Flow and Diffusion Models

🖌 随着生成的模型发展，Diffusion 的方法论，也变得越来越系统了，当然介绍相关知识的文档，也层出不穷。这个文档，我由数学到应用，解释当下 Flow Model，Diffusion Model 的原理和具体实现。除此之外，这个Blog主要是想将原来那套Stable Diffusion的描述语言和现在Flow Matching这套描述语言统一起来。

备注：Blog中的一些可视化脚本都在https://github.com/anschen1994/flow-diffusion# 这个仓库中

何为生成

首先在具体谈论数学模型之前，我们可以思考一下，生成在数学上是在做怎么样的一件事情。归根结底，生成在某种意义上就等价于数学上的“采样”。举个简单例子，我需要生成一张房屋的图片。那其实在数学上我们要做得事情：

找出 $p(\cdot|house)$，condition on 房屋的整个图片的概率分布是什么样子的。
从$p(\cdot|house)$,从上面的这个条件概率中去采样一个样本出来即可。

但是，我们往往没有办法知道$p(\cdot|house)$这个分布是什么样子的，因此，整个事情就没有办法很好的实施。那现在主流的生成所采取的方案，尝试建立某种简单初始分布（一般为高斯分布）和目标分布之间的转移方式，就如下面图所示。

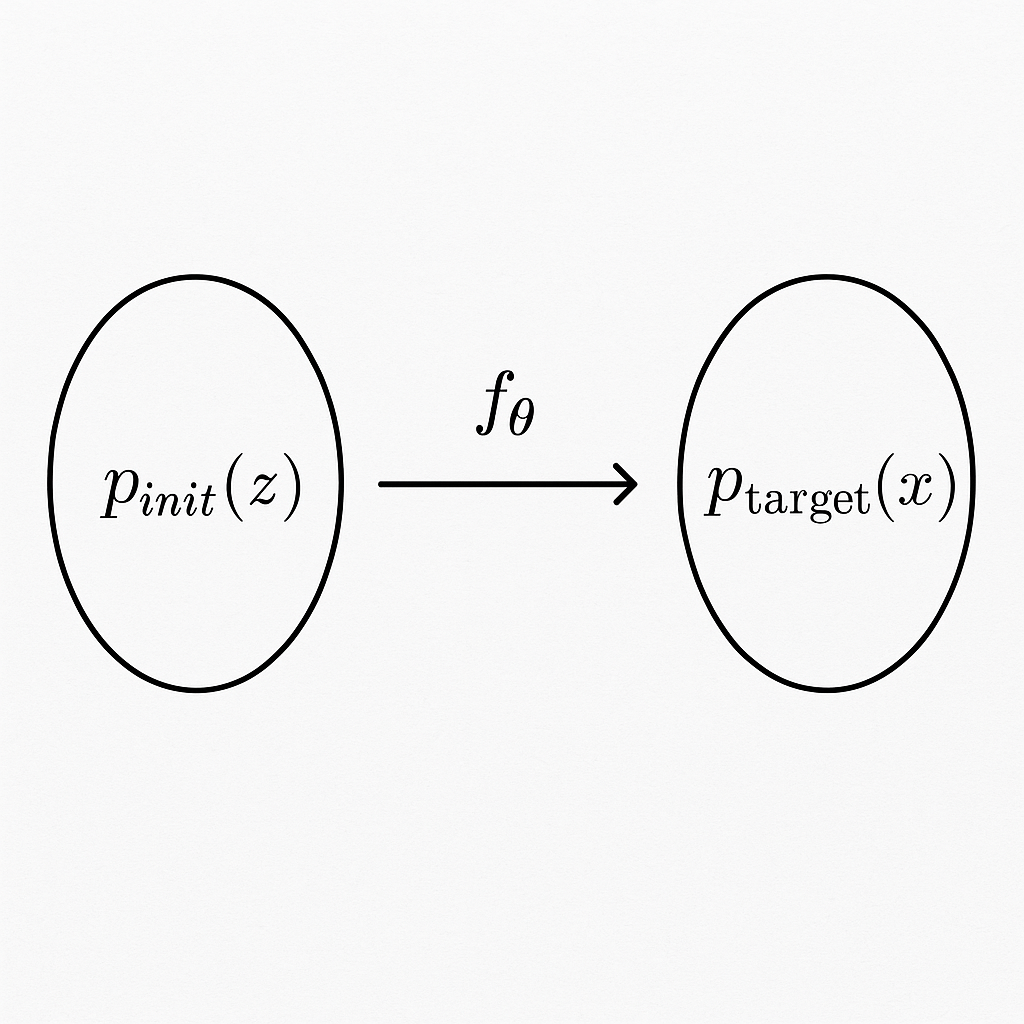
数学模型

Flow Model 和 Diffusion Model 也都是建立上面这种大致的想法上，诞生的两种算法。

首先无论是生成图片，视频，3D 模型等等，我们都可以将需要建模的对象，简化成一个高维的随机变量$X_t\in\mathbb{R}^d$

Flow Model

Flow Model 使用了简单的 ODE 去建立初始分布和目标分布之间的关系。

\[ \frac{dX_t}{dt}=f(X_t, t), t\in[0,1],\\ f:\mathbb{R}^d\times\mathbb{R} \to \mathbb{R}^d \]

同时满足

\[ X_0 \sim p_{init}, X_1 \sim p_{target} \]

所以对于简单的 Flow Model 来说，我们就是要找到$f(X_t,t)$去建立两个分布之间的联系。

当然这个模型被称之为 Flow Model 的原因。我们会将下面这种满足某个初始点的解称之为 Flow，即：

\[ \frac{d}{dt}\psi_t(x_0)=f(\psi_t(x_0),t),\psi_0(x_0)=x_0. \]

直观上来说$\psi_t(x_0), \psi_t(x_1), \psi_t(x_2), \cdots$ 就构成了初始点在$x_0,x_1,x_2,\cdots$的一些流，同时这些流在某些时空点$(x,t)$处，有的密集，有的稀疏。

Example

下面用一个简单的二维向原点收缩的例子，来可视化这个问题。

\[ \frac{dX_t}{dt}=-\theta X_t, X_0 \sim \mathcal{N}(0,5), t\in[0,1] \]

这个方程的解可以写成：

\[ X_t = e^{-\theta t}X_0 \]

对应的 flow 为

\[ \psi_t(x) = e^{-\theta t}x \]

从下面这个图，我们展现上面 Flow Model 对应的速度，其速度向量，都是沿着自身的反方向指向原点。

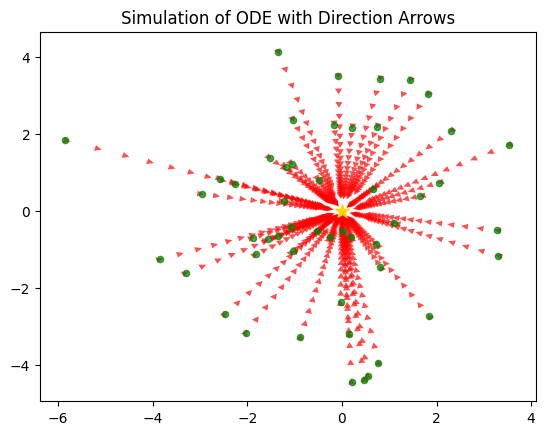
我们也可以用简单的 ODE 数值求解方法，并且可视化上面的各种 Flow $\psi_t(x)$，如下图:

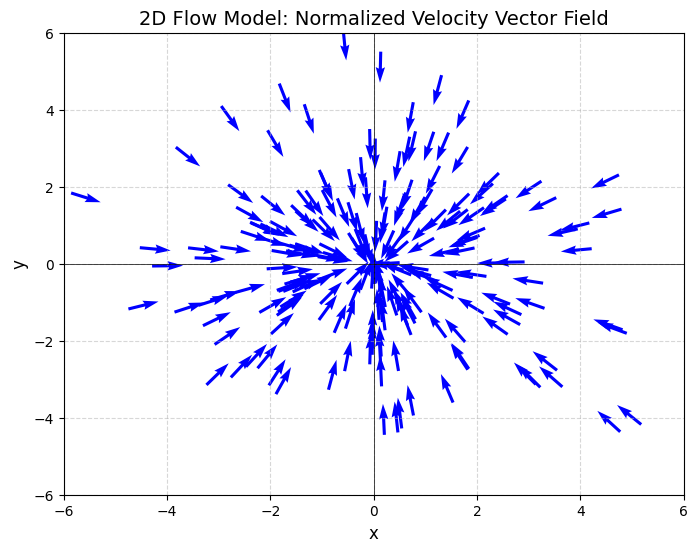
这个图中，每个绿点对应初始的$x$, 每个红色轨迹，对应着一条 flow $\psi_t(x)$.

Diffusion Model

在 Flow Model 中，我们发现整个动力学过程，没有随机性，可以用一个简单的 ODE 描述。Diffusion Model 则是在 Flow Model 的基础上，增加了一些随机过程，整体的动力学过程可以用下面的 SDE 描述:

\[ dX_t = f(X_t, t)dt + g(X_t, t)dW_t \]

这边的$dW_t$来自于经典的布朗运动，简单来说$dW_t$描述了一个方差为$dt$,均值为 0 的随机扰动。具体数学可以参见，任意介绍随即微积分的教材。

这边我们就需要注意到对于任意固定的$x$，我们不再会有一个确定性的流$\psi_t(x)$，因为就算初始点确定，整个过程依然充满了随机。

Example

我们扩展一下上面那个简单的 Flow Model，到经典的 OU(Ornstein-Uhlenbeck) Process.

\[ dX^{OU}_t = -\theta X_t dt + \sigma dW_t \]

我们可以知道上面 SDE 的解可以写成下面的积分形式：

\[ X^{OU}_t = e^{-\theta t}X_0 + \sigma \int_0^t e^{\theta(s-t)}dW_s \]

对比上面的 ODE，我们可以看到两者的数学期望是在任意时刻都是一样的，$\mathbb{E}[X_t^{OU}]=\mathbb{E}[X_t]=e^{-\theta t}X_0$. 但是$X^{OU}_t$存在明显的随机项，当然通过简单的计算，我们可以知道：

\[ \mathbb{Var}[X_t^{OU}] = \frac{\sigma^2}{2\theta}(1-e^{-2\theta t}), \mathbb{Cov}[X_t^{OU},X_s^{OU}]=\frac{\sigma^2}{2\theta}(e^{-\theta|t-s|}-e^{-\theta|t+s|}) \]

Flow and Diffusion Model 从上面的描述我们可以知道，Flow和Diffusion Model都可以使用下面对于随机变量的动力学方程描述: \[dX_t = f(X_t, t)dt + g(X_t, t)dW_t\] Flow Model 只是上面\[g(X_t,t)\equiv0\]的特殊情况

在下面的这张图中，我们可视化了 OU 过程：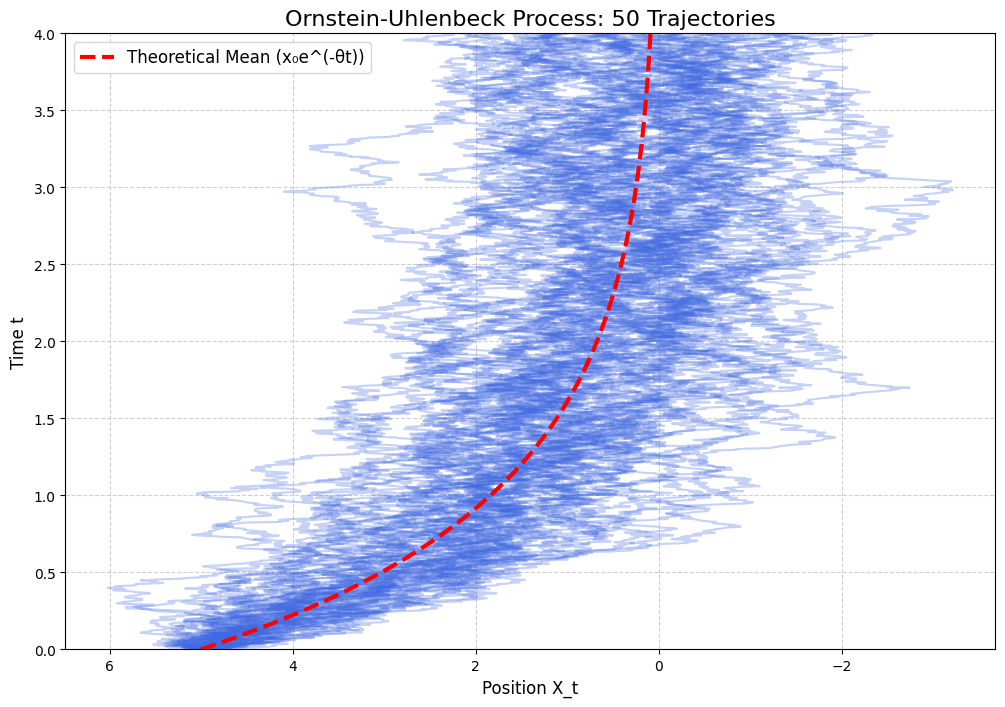

从$X_0=5$出发，给出了这个 SDE 对应的 50 条可能的 trajectory，同时用红色虚线，标注了这些轨迹对应的平均值$e^{-\theta t}X_0$

Fokker-Planck Equation

定理

Fokker-Planck Equation 是描述整个 Flow Model 和 Diffusion Model 的数学基石。这边主要陈列其几个重要的结果，具体的数学推导可以参考这个 Blog: https://www.peterholderrieth.com/blog/2023/The-Fokker-Planck-Equation-and-Diffusion-Models/

Fokker-Planck Equation 对于一个随机变量其动力学方程满足:\[dX_t=f(X_t,t)dt+g(X_t,t)dW_t\],当且仅当其随机变量对应的分布$p_t(x)$满足下面的动力学方程: \[\frac{dp_t(x)}{dt}=-\nabla\cdot(f(x,t)p_t(x))+\frac{1}{2}\nabla^2\cdot(g(x,t)g(x,t)^Tp_t(x))\]

上面方程第一项比较好理解，对于连续不可压缩的物质来说，散度$\nabla\cdot(f(x,t)p_t(x))$对应在时空点$(x,t)$处的净流量。第二项则是由$dW_t$这个布朗运动带来的。从直觉我们可以知道其大概的 scaling 由方差造成$dW_t^Tg^TgdW_t\sim gg^T I_d dt$。

Fokker-Planck Equation 最重要的点，是其成功连接了随机变量的动力学和其分布对应的动力学之间的关系

Example

这边我们以 OU Process 为例，解释 Fokker-Planck Equation。

首先 OU Process 的 FPE 可以写成下面的形式:

\[ \partial_t p_t(x)=\theta\partial_x(xp_t(x))+\frac{1}{2}\sigma^2\partial_x^2p_t(x) \]

上面这个 PDE 对应的解为(具体数学推导可以参考附录)，

\[ p_t(x)=\frac{1}{2\pi s_t^2}\exp\left(-\frac{(x-\mu_t)^2}{2s_t^2}\right), s_t^2:=\frac{\sigma^2}{2\theta}(1-e^{-2\theta t}),\mu_t:=x_0e^{-\theta t} \]

从这边我们可以看到$p_t(x)$对应的分布，和上面我们直接求解 SDE 是一样，是一个均值为$\mu_t$,标准差为$s_t$的高斯分布。

我们通过模拟 OU Process 从$t=0$到$t=4$50000次，同时记录$t=0.0,0.5,1.5,4.0$ 四个时间点的取值分布，并且根据 FPE 对应的解析解进行对比：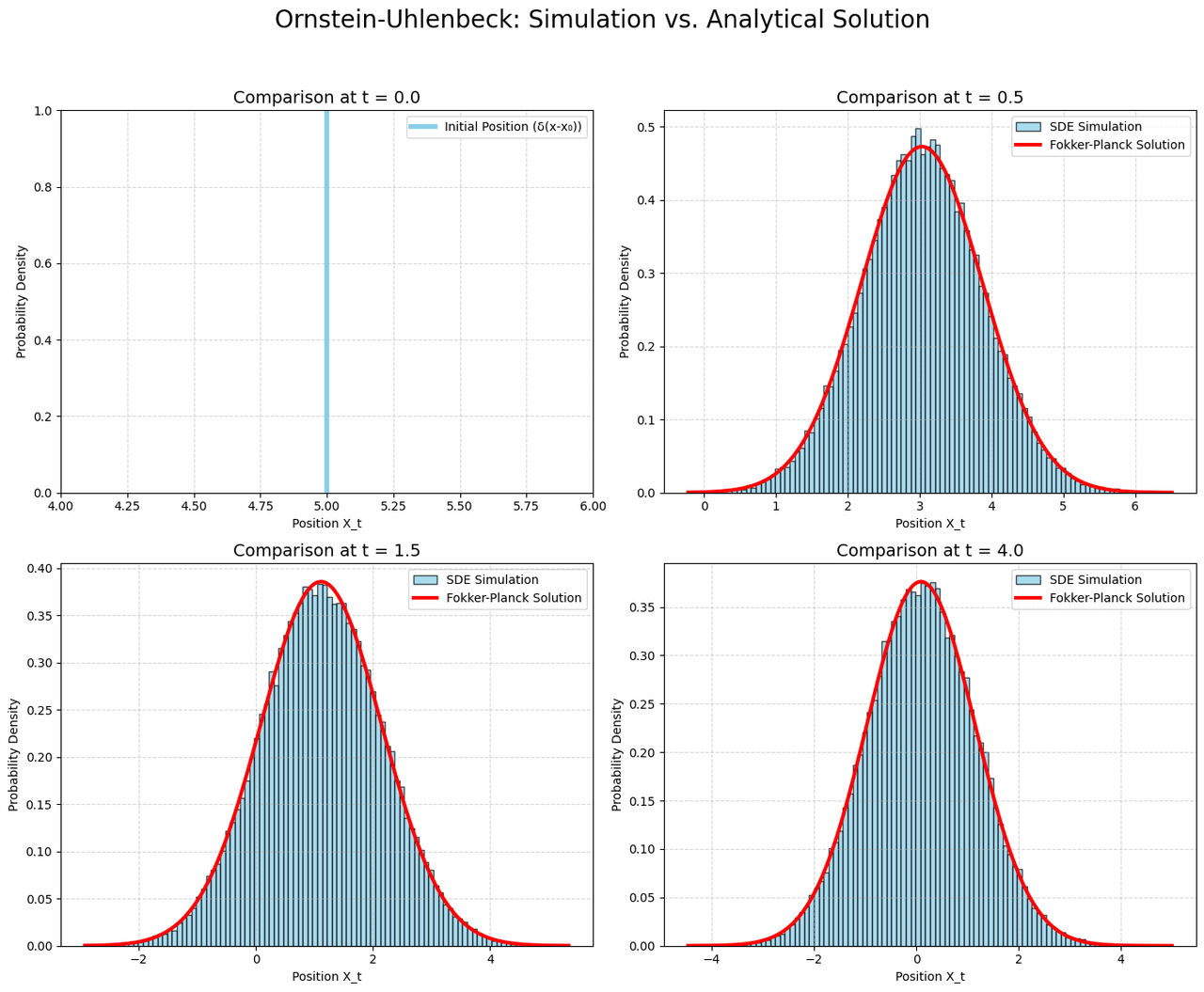

From SDE to ODE

From SDE to ODE 对于一个SDE $dX_t=f(X_t, t)dt+g(X_t,t)dW_t$, 我们可以找到一个ODE: \[dZ_t=F(Z_t,t)dt, \\ F(z,t):=f(z,t)-\frac{1}{2}\nabla\left(g(z,t)g(z,t)^T\right)-\frac{1}{2}g(z,t)g(z,t)^T\nabla \log p_t(z)\] 使得$X_t$在$t$时刻的分布$p_t(x)$和$Z_t$在$t$时刻的分布$p_t(z)$是一样的，如果他们的初始分布一样$X_0\sim p_{init}, Z_0\sim p_{init}$

上面这个方程考虑了比上面参考的 Blog 更一般的情况，因此多出来了额外的一项$-\frac{1}{2}\nabla\left(g(z,t)g(z,t)^T\right)$

上面这个定理告诉了我们一个很重要的事情，如果我们可以知道$\nabla \log p_t(x)$，那么就可以把 SDE 转化成 ODE。换句话说，如果我们知道$\nabla\log p_t(x)$, 那么我们从 Flow Model 得出来的结论很容易直接推广到 Diffusion Model

Example

我们仍然以 OU Process 来说明这个过程。

我们可以根据上面的这个定理知道，OU Process 对应的 ODE 应该可以写成这种形式：

\[ dZ_t=-\theta Z_tdt-\frac{1}{2}\sigma^2\partial_z\log p_t(Z_t)dt \]

如果$p_{init}$是一个高斯分布的话，比如$X_0\sim\mathcal{N}(\mu_0,\sigma_0)$，我们知道$X_t$也是服从一个高斯分布：

\[ X_t\sim\mathcal{N}(\mu_t,\sigma_t),\mu_t=\mu_0e^{-\theta t},\sigma_t^2=\sigma_0^2e^{-2\theta t}+\frac{\sigma^2}{2\theta}(1-e^{-2\theta t}) \]

我们可以知道其对应的 ODE 是：

\[ dZ_t = -\theta Z_t dt+\frac{\sigma^2}{2}\frac{Z_t-\mu_t}{\sigma_t^2}dt \]

下面是通过一个 Python 程序来描述了这个过程。

Reversed Time SDE

Reversed Time SDE 对于一个SDE: \[dX_t=f(X_t, t)dt+g(X_t,t)dW_t\]$t$从$0$到$1$的演化用这个方程描述。那么$\tau:=1-t$从$1$到$0$的演化，则可以用下面的方程描述: \[d\overleftarrow{X}_{\tau}=\overleftarrow{f}(\overleftarrow{X}_{\tau},\tau)d\tau+g(\overleftarrow{X}_{\tau},\tau)dW_{\tau},\\ \overleftarrow{f}(x,\tau)=-f(x,t)+\nabla (g(x,\tau)g(x,\tau)^T)+g(x,\tau)g(x,\tau)^T\nabla\log p_{\tau}(x)\]

关于上面的定理的证明，一般都是采用 Kolmogorov Forward Equation 和 Kolmogorov Backward Equation 去获得$p(x,t|y,s)$这样的联合分布，然后在求得对应的边际分布。整体正面思路稍显复杂，这边借助 Fokker-Planck Equation 在附录给出一个稍微简单点的数学证明。

Example

我们这边仍然以简单的 OU Process 作为例子来阐述上面这个定理。对于 OU Process，我们可以知道：

\[ \overleftarrow{f}(x,\tau)=\theta x - \sigma^2 \frac{x -\mu_{1-\tau}}{\sigma_{1-\tau}^2} \]

我们通过一些 Python 代码去可视化，上面这个过程确实是反向过程：

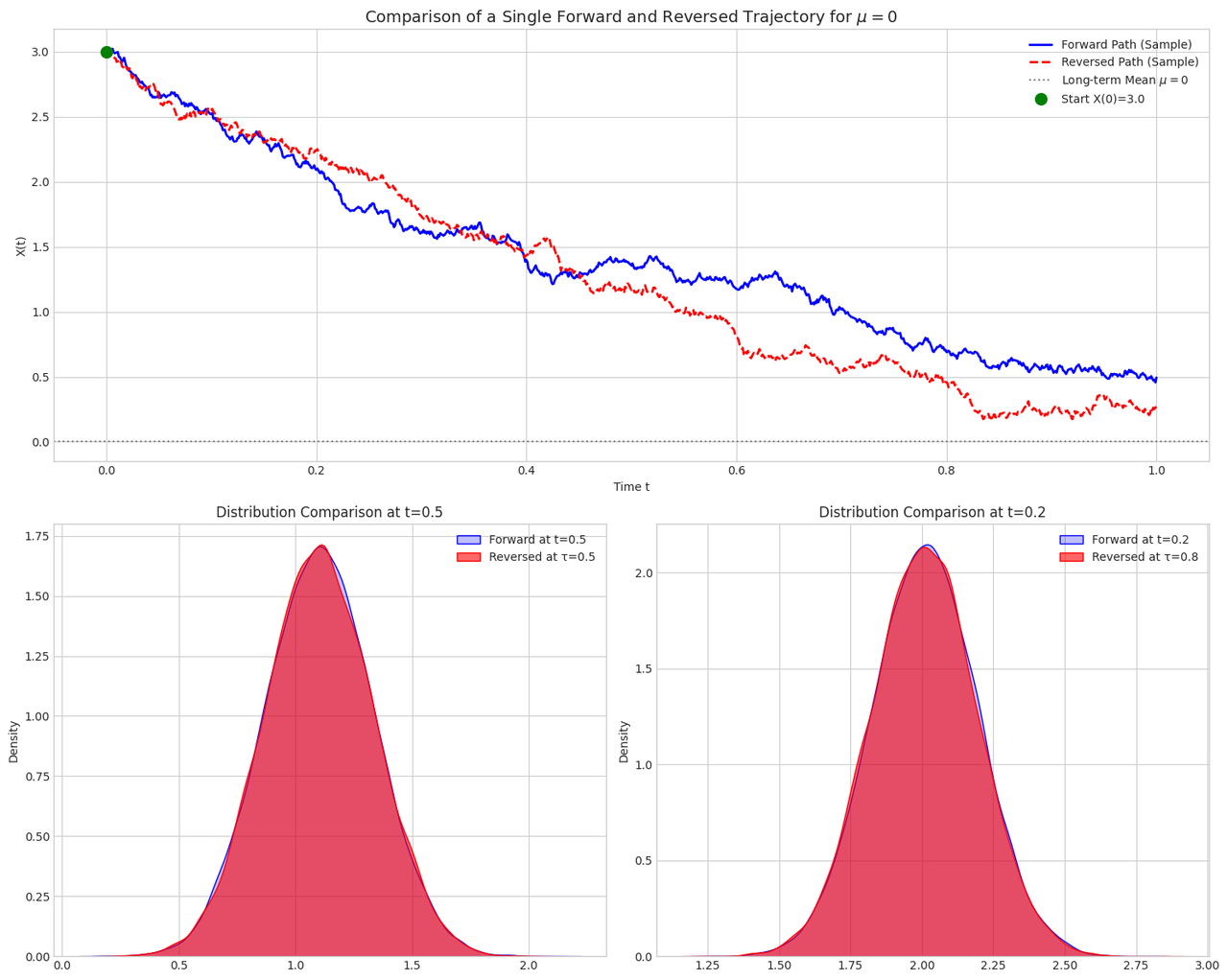
从下面这个分布上看，我们可以明显看到反向过程在$\tau$时刻的分布和正向过程在 $1-\tau$ 时刻的分布是一样的。

不过我们注意到一个非常有意思的点，从这张图的上半部分，可以看到反向过程，神奇地重新收敛回$x_0$，无论是你从怎么样的$x_1$开始去做这个方向过程。

我们这边对于此，给出一个比较简单是粗糙的分析，这个现象是如何发生的。我把$\overleftarrow{f}(x,\tau)$在$\tau=1$处做展开，其等价于$\overleftarrow{f}(x,t)$ 在$t=0$处做展开。

\[ \overleftarrow{f}(x,t)=\theta x - \frac{2\theta(x-x_0e^{-\theta t})}{1-e^{-2\theta t}}\approx \theta x -\frac{2\theta(x-x_0+x_0\theta t)}{2\theta t} \sim \frac{x-x_0}{t} \]

在$t\sim 0$的时候，会有一个无穷大的力，将其拽回$x_0$.

神经网络的引入

当然在 AIGC 领域，一般不会考虑上面这么复杂的 SDE，其往往考虑简单的各向同性的 SDE，后续的讨论，我们也将只讨论下面这张稍微简化点的版本:

\[ dX_t=f(X_t,t)dt+\sigma_t dW_t \]

当$\sigma_t\equiv 0$的时候，回退到 Flow Model.

有了上面的基础的概念，我们知道了一件事情，如果我们需要给$p_{init}$和$p_{target}$这两个分布，找出一个连接的桥梁，那么只需要找出满足一个满足条件的 ODE(Flow Model)或者 SDE(Diffusion Model)。但是比较困难的时候，我们怎么找到这些的 SDE 或者 ODE 呢？这个时候就神经网络的登场的时候，当我们不知道具体的动力学方程该怎么写的时候，那么就可以使用神经网络代替他，然后找到一个好的 Loss 去优化。

第一步，

既然不知道什么样的$f(X_t,t)$可以正确连接$p_{init}$和$p_{target}$，那么我们就用神经网络代替他，

\[ dX_t=f_{\theta}(X_t,t)dt+\sigma_t dW_t \]

第二步，我们需要构造怎么样的 Loss 来训练$f_{\theta}(x,t)$呢。这边很自然地会想到:

直接找到$f(x,t)$对应的值$\tilde{f}(x,t)$，然后使用 MSE Loss 去拟合:

\[ \min_{\theta}\mathbb{E}_{X_t}[\|f_{\theta}(X_t,t)-\tilde{f}(X_t,t)\|^2] \]

Flow Model

首先直接想要知道$\tilde{f}(x,t)$长什么样子是非常困难的，因为不太知道$p_{target}$（即$p_{data}$）具体是什么样子。但是如果对于某个样本$z \sim p_{data}$，好在我们是比较容易知道$\tilde{f}(x,t|z)$是什么样子的。

Gaussian Probability Path 具体个简单的例子，假设初始分布是一个高斯分布并且$\sigma_t=0$，我们可以假设分布函数$p_t(x|z)$由下面的形式给出来： \[x_t=\alpha_t z + \beta_t \epsilon, \epsilon \sim \mathcal{N}(0,I_d), \\\alpha_0:=0,\alpha_1:=1,\beta_0:=1,\beta_1:=0\\ x_t \sim p_t(x|z)\] 很显然上面这个过程满足$p_0(x|z)=\mathcal{N}(0,I_d),p_1(x|z)=\delta(x-z)$, 那么： \[p_0(x)=\int p_{data}(z)\mathcal{N}(0,I_d)dz = \mathcal{N}(0,I_d),\\ p_1(x)=\int p_{data}(z)\delta(x-z)dz = p_{data}(x)\] 因此这是一个合理的构造。那么对于这样的构造，它对应的$\tilde{f}(x,t|z)$长什么样子呢。那么只需要简单将上面的过程带入ODE, \[\tilde{f}(x_t,t|z)=\frac{dx_t}{dt}=\dot{\alpha_t}z+\dot{\beta_t}\epsilon\] 那么找出函数$\tilde{f}$满足上述的方程，那么我们知道$x_t=\alpha_t z+\beta_t \epsilon$, 经过简单的调整我们就知道： \[\tilde{f}(x_t,t|z)=\dot{\alpha_t}z+\dot{\beta_t}\epsilon=\dot{\alpha_t}z+\dot{\beta_t}\frac{x_t-\alpha_t z}{\beta_t}=(\dot{\alpha_t}-\frac{\dot{\beta_t}}{\beta_t}\alpha_t)z+\frac{\dot{\beta_t}}{\beta_t}x_t\]

那么当我们有了$\tilde{f}(x,t|z)$，我们才能知道$f(x,t)$呢？这个时候 Fokker-Planck 就可以派上用场了。我们知道$f(x,t)$，需要满足下面的方程:

\[ \frac{dp_t(x)}{dt}=-\nabla\cdot(\tilde{f}(x,t)p_t(x)) \]

而方程左边可以写成

\[ \frac{dp_t(x)}{dt}=\int \frac{dp_t(x|z)}{dt}p_{data}(z)dz \\ = -\int \nabla \cdot (p_t(x|z)\tilde{f}(x,t|z))p_{data}(z)dz \\ = -\nabla \cdot \int p_t(x) \frac{p_t(x|z)}{p_t(x)}\tilde{f}(x,t|z)p_{data}(z)dz \]

对比这两个方程，我们就可以知道：

\[ \tilde{f}(x,t)=\int \tilde{f}(x,t|z)\frac{p_t(x|z)}{p_t(x)}p_{data}(z)dz \]

因此，对应的 Loss 可以写作如下的形式：

\[ \mathcal{L}=\mathbb{E}_{t,x\sim p_t(x)}\left[\left(f_{\theta}(x,t)-\tilde{f}(x,t)\right)^2\right] \]

但是上面这个 Loss，实际上不太可以使用，因为$\tilde{f}(x,t)$需要我们对$p_{data}(z)$这个实际我们不知道的分布进行积分。因此在实际操作的过程中，我们往往对数据进行采样，去近似这个积分：

\[ \mathcal{L}_{cond}=\mathbb{E}_{t,z\sim p_{data}, x\sim p_t(x|z)}\left[\left(f_{\theta}(x,t)-\tilde{f}(x,t|z)\right)^2\right] \]

Diffusion Model

那么根据 Flow and Diffusion Models，我们直接将 Flow Model 和 Diffusion Model 连接起来。如果我们的目标是找到一个 SDE$dX_t=F(X_t,t)dt+\sigma_tdW_t$，使得其在$t$时刻的概率分布为$p_t(x)$那么可以知道：

\[ F(x,t)=f(x,t)+\frac{1}{2}\sigma_t^2\nabla \log p_t(x) \]

对于$f(x,t)$相关的 Loss 则是和上面 Flow Model 是一样的。那么我们只需要另外一个神经网络$s_{\theta}(x,t)$去拟合$\nabla p_t(x)$。类似上面的推导，我们可以条件 Loss：

\[ \mathcal{L}_{cond}^{score}=\mathbb{E}_{t,z\sim p_{data}, x\sim p_t(x|z)}\left[\left(s_{\theta}(x,t)-\nabla \log p_t(x)\right)^2\right] \]

Gaussian Probability Path训练过程 对于GPP这种过程，我们可以知道： \[\mathcal{L}_{cond}=\mathbb{E}_{t,z\sim p_{data}, x\sim p_t(x|z)}\left[\left\|f_{\theta}(x,t)-(\dot{\alpha_t}-\frac{\dot{\beta_t}}{\beta_t}\alpha_t)z-\frac{\dot{\beta_t}}{\beta_t}x\right\|^2\right] \\ \mathcal{L}_{cond}^{score}=\mathbb{E}_{t,z\sim p_{data}, x\sim p_t(x|z)}\left[\left\|s_{\theta}(x,t)+\frac{x-\alpha_t z}{\beta_t^2}\right\|^2\right]\] 关于上面这个Loss，我们可以换两个角度去看待。第一，我们可以从噪声的角度去看，$x \sim p_t(x|z)$，$x$从这个分布里面去采样，真正决定$x$值的其实就是高斯造成$\epsilon$通过$x_t=\alpha_t z+\beta_t \epsilon$，那么我们可以将上面的Loss重新表示成: \[\mathcal{L}_{cond}^{score}=\mathbb{E}_{t,z\sim p_{data},\epsilon \sim \mathcal{N}(0,I_d)}\left[\left\|s_{\theta}(x,t)+\frac{\epsilon}{\beta_t}\right\|^2\right]\] 而传统Diffusion Model的Loss，常常写成如下的形式： \[\mathcal{L}_{SD}=\mathbb{E}_{t,z,\epsilon}\left[\left\|\epsilon_{\theta}(x_t,t)-\epsilon\right\|^2\right]\] 这边我们就可以看出来：Score Matching和Diffusion Model原本使用variational lower bound这种近似方法，殊途同归了。 第二，观察到对于GPP来说, \[(\dot{\alpha_t}-\frac{\dot{\beta_t}}{\beta_t}\alpha_t)z+\frac{\dot{\beta_t}}{\beta_t}x_t=\dot{\alpha_t}z+\dot{\beta_t}\epsilon=\frac{\dot{\alpha_t}}{\alpha_t}x_t-(\frac{\dot{\alpha_t}}{\alpha_t}\beta_t-\dot{\beta_t})\epsilon\] 那么，这个是如果我们训练出来了一个很好的score function,$s_{\theta}(x,t)$可以很好拟合$\epsilon$,那么我们不再需要训练额外的$f_{\theta}(x,t)$。 换句话说：对于GPP来说，只需要做Score matching，训练$s_{\theta}(x,t)$就足够了。

离散时间的 Diffusion Model

DDPM 简介

在 Diffusion Model 刚刚在 AIGC 领域兴起的时候，整体的描述语言，并不是上面这样。而是以离散时间的布朗运动来描述，整个过程分为：

Forward Diffusion Process（前向过程）
Reverse Diffusion Process （逆向过程）

具体的描述可以参考下面这个非常好的 Blog：https://lilianweng.github.io/posts/2021-07-11-diffusion-models/

我们这边只陈列一些 Notation 和重要的结论。

Forward Diffusion Process

\[ x_0\to x_1 \to x_2 \to \cdots x_N \to \cdots \]

每一步使用一个 Gaussian 随机变量去加噪:

\[ x_n=\sqrt{\alpha_n}x_{n-1}+\sqrt{1-\alpha_n}\epsilon;x_0 \sim p_{data},x_{+\infty}\sim \mathcal{N}(0,I_d) \]

这边我们全部使用$n$代替，因为整个过程是离散的。同时利用 Gaussian 分布的关系，$x_n,x_0$之间的关系可以表示为:

\[ x_n=\sqrt{\bar{\alpha}_n}x_0+\sqrt{1-\bar{\alpha}_n}\epsilon, \bar{\alpha}_n=\prod_{i=1}^n\alpha_i \]

Reverse Diffusion Process

\[ \cdots \to x_N \to x_{N-1} \to \cdots x_1 \to x_0 \]

在给定$x_0$的时候，可以得到逆向的条件分布:

\[ p(x_{n-1}|x_n,x_0) \sim \mathcal{N}(\tilde{\mu}(x_n,x_0),\tilde{\sigma}_n I_d),\\ \tilde{\mu}(x_n, x_0)=\frac{\sqrt{\alpha_n}(1-\bar{\alpha}_{n-1})}{1-\bar{\alpha}_n}x_n+\frac{\sqrt{\bar{\alpha}_{n-1}}\beta_n}{1-\bar{\alpha}_n}x_0=\frac{1}{\sqrt{\alpha_n}}\left(x_n-\frac{1-\alpha_n}{\sqrt{1-\bar{\alpha}_n}}\epsilon\right),\\ \tilde{\sigma}_n=\frac{1-\bar{\alpha}_{n-1}}{1-\bar{\alpha}_n}\beta_n \]

损失函数

简化过后的损失函数

\[ \mathcal{L}_{simple}=\mathbb{E}_{n,x_0,\epsilon_n}\left[\left\|\epsilon_{\theta}(\sqrt{\bar{\alpha}_n}x_0+\sqrt{1-\bar{\alpha}_n}\epsilon_n, n)-\epsilon_n\right\|^2\right] \]

DDIM

DDIM 的进步之处

当然 DDPM 整个过程，最核心的点是，给定一个$n$，那么随机变脸$X_n$需要满足如下的分布：

\[ x_n\sim\mathcal{N}(\sqrt{\bar{\alpha}_n}x_0,\sqrt{1-\bar{\alpha}_n}I_d) \]

在 DDPM 中整个过程都是马尔可夫的。但是实际上，如果只是满足上面这个分布的话，那整个过程不一定需要马尔可夫的。可以证明的是，如果

\[ p(x_{n-1}|x_n,x_0)=\mathcal{N}\left(\sqrt{\bar{\alpha}_{n-1}}x_0+\sqrt{1-\bar{\alpha}_{n-1}-\sigma_n}\frac{x_n-\sqrt{\bar{\alpha}_n}x_0}{\sqrt{1-\bar{\alpha}_n}}, \sigma_nI_d\right) \]

那么上面的过程分布就能被满足。

第一，我们可以看到如果${\sigma}_n=\frac{1-\bar{\alpha}_{n-1}}{1-\bar{\alpha}_n}\beta_n$，那么这个表达式则回退到 DDPM 的情况。

第二，如果我们令$\sigma_n\equiv0$，那么，

\[ p(x_{n-1}|x_n,x_0)=\delta_{x_{n-1}}\left(\sqrt{\bar{\alpha}_{n-1}}x_0+\sqrt{1-\bar{\alpha}_{n-1}}\frac{x_n-\sqrt{\bar{\alpha}_n}x_0}{\sqrt{1-\bar{\alpha}_n}}\right)=\delta_{x_{n-1}}\left(\sqrt{\bar{\alpha}_{n-1}}x_0+\sqrt{1-\bar{\alpha}_{n-1}}\epsilon\right) \]

变成了一个确定性的过程。

第三，同时生成的过程中，我们需要注意到一件非常好的事情。加入我们已经训练好了$\epsilon_{\theta}$，我们不需要像 DDPM 那样，先从 Gaussion 中采样一个$x_N$然后一步一步的使用$\epsilon_{\theta}(x_n,n)$去去除噪声。而是可以根据上看这个表达式去优化生成的过程，因为我们核心关心的只是$p(x_{n-1}|x_n,x_0)$这个边际分布。首先我们发现要确定$x_{n-1}$,不仅要知道$x_n$，还要知道$x_0$，但是在生成过程中，我们是不知道$x_0$是多少的，因此最简单的一个原则，是使用估计的$\hat{x}_0$去代替上面公式的$x_0$，因此：

\[ x_{n-1}=\sqrt{\bar{\alpha}_{n-1}}\hat{x}_0+\sqrt{1-\bar{\alpha}_{n-1}-\sigma_n}\epsilon_{\theta}(x_{n},n)+\sigma_n\epsilon,\\ \hat{x}_0=\frac{x_n-\sqrt{1-\bar{\alpha}_n}\epsilon_{\theta}(x_n,n)}{\sqrt{\bar{\alpha}_n}} \]

与 Flow Model 的联系

DDPM

首先我们先分析一下 DDPM，对于 DDPM 来说，他的 Forward Process 为:

\[ x_n=\sqrt{\alpha_n}x_{n-1}+\sqrt{1-\alpha_n}\epsilon;x_0 \sim p_{data},x_{+\infty}\sim \mathcal{N}(0,I_d) \]

那么对于一个固定的$N$，我们可以令$t_n=\frac{n}{N},\Delta t=\frac{1}{N}$，将上面的方程 rescale 到$[0,1]$，因此：

\[ x_{t+\Delta t}=\sqrt{\frac{\bar{\alpha}_{t+\Delta t}}{\bar{\alpha}_t}}x_t+\sqrt{1-\frac{\bar{\alpha}_{t+\Delta t}}{\bar{\alpha}_t}}\epsilon \]

对上面的式子，做展开，保留到 $\Delta t$，我们可以得到:

\[ dx_t=\frac{1}{2}\frac{\dot{\bar{\alpha}_t}}{\bar{\alpha}_t}x_t+\sqrt{-\frac{\dot{\bar{\alpha}_t}}{\bar{\alpha}_t}dt}\epsilon \]

这边我知道 $\bar{\alpha}_t$ 是随着时间单调递减，因此 $\dot{\bar{\alpha}}_t<0$。当然为了保持和 Paper 里面的一致，如果我们定义:$\beta_t=-\frac{d}{dt}\log\bar{\alpha}_t$，那么我们就可以得到比较熟悉的 Foward Process 对应的 SDE:

\[ dX_t=-\frac{1}{2} \beta_t X_t dt+\sqrt{\beta_t}dW_t \]

其对应的 Reversed Time SDE 则可以写成:

\[ d\overleftarrow{X}_{\tau}=\left(\frac{1}{2}\beta_{\tau}\overleftarrow{X}_{\tau}+\beta_{\tau}\nabla \log p_{\tau}(\overleftarrow{X}_{\tau})\right)d\tau+\sqrt{\beta_{\tau}}dW_{\tau} \]

或者：

\[ d\overleftarrow{X}_{t}=-\left(\frac{1}{2}\beta_{t}\overleftarrow{X}_{t}+\beta_{t}\nabla \log p_{t}(\overleftarrow{X}_{t})\right)dt+\sqrt{\beta_{t}}d\overleftarrow{W}_{t} \]

根据 Fokker-Planck Equation，我们知道这个 SDE 对应的 ODE，可以写成:

\[ d\overleftarrow{X}_{t}=-\frac{1}{2}{\beta}_{t}\overleftarrow{X}_{t}dt-\frac{1}{2}{\beta}_{t}\nabla \log p_{t}(\overleftarrow{X}_{t})dt \]

因此这个会是上面 Diffusion Model 的一种特殊的情况。

DDIM

另外对于 DDIM，从直觉上看起来，如果$\sigma_n\equiv 0$，上面整个生成过程也是一个确定性的过程。而我们之前介绍的 Flow Model 也是确定性的，那么这两个在本质上是不是同一个事情呢。

根据上面的手法，我们可以直接将，DDIM 的生成离散化，得到一个 SDE。

其离散的方程为:

\[ x_{n-1}=\sqrt{\bar{\alpha}_{n-1}}\frac{x_n-\sqrt{1-\bar{\alpha}_n}\epsilon_{\theta}(x_n,n)}{\sqrt{\bar{\alpha}_n}}+\sqrt{1-\bar{\alpha}_{n-1}}\epsilon_{\theta}(x_{n},n) \]

对应的连续展开为:

\[ x_{t-dt}=\sqrt{\frac{\bar{\alpha}_{t-dt}}{\bar{\alpha}_t}}\left(x_t-\sqrt{1-\bar{\alpha}_t}\epsilon_{\theta}\right)+\sqrt{1-\bar{\alpha}_{t-dt}}\epsilon_\theta \\ = (1-\frac{1}{2}\frac{\dot{\bar{\alpha}_t}}{\alpha_t}dt)x_t-d\sqrt{1-\bar{\alpha}_t}\epsilon_{\theta}+\frac{1}{2}\frac{\dot{\bar{\alpha}_t}}{\alpha_t}dt\sqrt{1-\bar{\alpha}_t}\epsilon_{\theta} \]

当然，我们利用$\frac{d}{dt}\sqrt{1-\bar{\alpha}_t}=\frac{\dot{\bar{\alpha}}_t}{2\sqrt{1-\bar{\alpha}}_t}$,我们最终可以得到:

\[ dX_t=\frac{1}{2}\frac{\dot{\bar{\alpha}}_t}{\bar{\alpha}_t}X_tdt-\frac{1}{2}\frac{\dot{\bar{\alpha}}_t}{\sqrt{1-\bar{\alpha}_t}\bar{\alpha}_t}\epsilon_{\theta} \]

使用上面的符号:

\[ d\overleftarrow{X}_t=-\frac{1}{2}\beta_t\overleftarrow{X}_tdt+\frac{1}{2}\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_{\theta}(\overleftarrow{X}_t) \]

那么对比一下，我们就知道 DDIM 的$\epsilon_{\theta}$只需要拟合$-\frac{\nabla \log p_t(x)}{\sqrt{1-\alpha_t}}$，那么整个过程就是 DDPM 没有什么特别的区别，至少就整体的分布情况来说。而且事实上，对于 GPP 来说，神经网络就是在拟合整个 score function.

Conditional Generation

上面我们主要讨论的还是，如果去构建$p_{init}$到$p_{target}$之间的映射，这样通过对于$p_{init}$进行采用，达到在$p_{target}$里面采样的效果，即所谓的生成。但是在现实中，我们应用的时候，我们都是输入一个 prompt 或者某种条件，以此保证 AI 可以生成符合要求的图像、视频，而不是直接从全集中采样一个图像或视频。

那么上面的训练过程则可以变成:

输入某一个 prompt 或者条件$c$
根据对应的条件$c$，去采样一个真实的样本$z_c$
使用神经网络$f_{\theta}(x|c)$去拟合$\tilde{f}(x|z_c)$

那么这边我们就会发现一件比较重要的事情，我们可以通过控制$c$的采样，去控制$z_c$的采样结果，这样我们就可以影响最终的训练效果。因此，我们需要对上面的过程做一个拆解，拆解成两部分，一部分完全不受$c$采样算法的影响，一部分可以$c$的采样算法进行调控。

对于 GPP 来说，我们知道$f_{\theta}(x|c)$拟合的目标是$\frac{\dot{\beta}_t}{\beta_t}x_t+(\dot{\alpha_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t})z_c$，我们可以经过一些变化，把这个重新写成：

\[ f_{\theta}(x|c) \to \frac{\dot{\alpha}_t}{\alpha_t}x + \frac{\dot{\alpha}_t\beta_t^2-\dot{\beta}_t\beta_t\alpha_t}{\alpha_t}\nabla \log p_t(x|z_c):=A_tx+B_t\nabla\log p_t(x|z_c) \]

我们还有：

\[ \nabla\log p_t(x|z_c)=\nabla\log \frac{p(z_c|x)p(x)}{p(z_c)}=\nabla\log p(x)+\nabla \log p(z_c|x) \]

这是因为$\nabla p(z_c)=0$。

因此,

\[ f_{\theta}(x|c)\to A_tx+B_t\nabla\log p(x)+B_t\nabla\log p(z_c|x)=\tilde{f}(x,t)+B_t\nabla\log p(z_c|x) \]

从上面这个结果，我们可以看到：

第一步是全局的速度场和你的采样没有关系
第二步则是类似一个分类或者 image caption 的任务

因此对于$c$采样算法对最终结果的影响，主要由第二部分造成。因此，可以我们可以通过一个超参数$\lambda$来控制这部分的影响。

\[ f_{\theta}(x|c)\to \tilde{f}(x,t)+\lambda B_t\nabla\log p(z_c|x) = \tilde{f}(x,t)+\lambda B_t(\nabla \log p(x|z_c) -\nabla\log p(x))\\ f_{\theta}(x|c) \to (1-\lambda)\tilde{f}(x,t)+\lambda\tilde{f}(x,t|z_c) \]

第一部分则是上面没有条件的拟合目标，第二部分则是有条件的拟合目标。当然我们不需要训练两个网络分别拟合，而是直接增加一个$\empty$来代表第一部分。因此最终的完整算法，可以用下面的过程来描述：

Classifier-free guidance CFM(CFG-CFM) - 训练： - 从$p_{data}$采样一组$(z_c,c)$ - $t\sim Uniform[0,1]$ - $x \sim p_t(x|z_c)$ - 以$p_{drop}$$丢弃掉条件$$c$$,即$$c=\empty$ - $\min_{\theta}\|f_{\theta}(x,t|c)-\tilde{f}(x|z_c)\|^2$ - 部署： - 给出一个条件$c$ - $x_0\sim p_{init}$ - 使用PDE数值方法求解$dX_t=f_{\theta}(x,t|c)dt$ - 得到$x_1$

附录

Reversed Time SDE 证明

对于一个 SDE:$dX_t=f(X_t,t)dX_t+g(X_t,t)dW_t$其对应的 Fokker-Planck Equation 是如下的形式：

\[ \frac{dp_t(x)}{dt}=-\nabla\cdot(f(x,t)p_t(x))+\frac{1}{2}\nabla^2\cdot(g(x,t)g(x,t)^Tp_t(x)) \]

如果我们单纯地想知道，对应地 Reversed Time SDE 长什么样子，我们可以使用简单地换元$\tau=1-t$，得到：

\[ \frac{dp_{\tau}(x)}{d\tau}=-\frac{dp_t(x)}{dt}=\nabla\cdot(f(x,\tau)p_{\tau}(x))-\frac{1}{2}\nabla^2\cdot(g(x,\tau)g(x,\tau)^Tp_{\tau}(x)) \]

根据简单地向量求导法则:

\[ \nabla^2\left(gg^Tp\right)=\nabla\cdot\left(\nabla(gg^Tp)\right)=\nabla\cdot\left(p\nabla(gg^T)+gg^T\nabla p\right)=\nabla\cdot \left[p\left(\nabla(gg^T)+gg^T\nabla \log p\right)\right] \]

那么根据 Fokker-Planck Equation 我们可以知道下面这个 ODE，可以用来描述 Reversed Time SDE:

\[ d\overleftarrow{X}_{\tau}=\left(-f(\overleftarrow{X}_{\tau},\tau)+\frac{1}{2}\nabla g(\overleftarrow{X}_{\tau},\tau)g(\overleftarrow{X}_{\tau},\tau)^T+\frac{1}{2}g(\overleftarrow{X}_\tau,\tau)g(\overleftarrow{X}_{\tau},\tau)^T\nabla\log p_{\tau}(X_{\tau})\right) \]

当然，同时根据 SDE 和 ODE 的关系 Flow and Diffusion Models，如果我们增加一个随机项$gdW$,那么我们需要在 shift 中补入:$\frac{1}{2}\nabla(gg^T)+\frac{1}{2}gg^t\nabla \log p$

因此完整的 Reversed Time SDE 可以写成下面的形式:

\[ d\overleftarrow{X}_{\tau}=\overleftarrow{f}(\overleftarrow{X}_{\tau},\tau)d\tau+g(\overleftarrow{X}_{\tau},\tau)dW_{\tau},\\ \overleftarrow{f}(x,\tau)=-f(x,t)+\nabla (g(x,\tau)g(x,\tau)^T)+g(x,\tau)g(x,\tau)^T\nabla\log p_{\tau}(x) \]

OU Process 对应的 FPE 的解

对于偏微分方程：

\[ \partial_t p_t(x)=\theta\partial_x(xp_t(x))+\frac{1}{2}\sigma^2\partial_x^2p_t(x) \]

该 PDE 设计到对于空间的二阶导数，一般习惯上会使用傅里叶变换，将其转化成代数方程，那么我们可以定义

\[ \tilde{p}_t(w):=\mathcal{F}[p_t(x)]:=\frac{1}{\sqrt{2\pi}}\int p_t(x)e^{-iwx}dx \]

根据傅里叶变换的基本性质：

\[ \mathcal{F}[xp_t(x)]=i\partial_w \tilde{p}_t(w),\mathcal{F}[\partial_x^2p_t(x)]=-w^2\tilde{p}_t(w) \]

变换之后的 PDE，变成了：

\[ \partial_t\tilde{p}_t(w)=-\theta w\partial_w\tilde{p}_t(w)-\frac{1}{2}\sigma^2w^2\tilde{p}_t(w) \]

该方程为一阶 PDE，因此我们可以使用传统的达朗贝尔方法求解：

\[ \frac{dt}{1}=\frac{dw}{\theta w}=-2\frac{d\tilde{p}}{\sigma^2w^2\tilde{p}} \]

从左边一半，可以得到$w=C_1e^{\theta t}$，从右边一半可以得到$\tilde{p}=C_2e^{-\frac{\sigma^2}{4\theta}w^2}$。因此我们可以得到，一个通用的解:

\[ \tilde{p}_t(w)=e^{-\frac{\sigma^2w^2}{4\theta}}F(we^{-\theta t}) \]

下面我们就需要根据边界条件去确认$F$的形式。

如果假设我们的初始分布为$p_0(x)=\delta(x-x_0)$，那么我们可以知道$\tilde{p}_0(w)=\frac{1}{\sqrt{2\pi}}e^{-iwx_0}$

那么我们有:

\[ F(w)=\frac{1}{\sqrt{2\pi}}e^{-iwx_0}e^{\frac{\sigma^2w^2}{4\theta}} \]

因此，我们有：

\[ \tilde{p}_t(w)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{\sigma^2w^2}{4\theta}(1-e^{-2\theta t})\right)\exp\left(-iwe^{-\theta t}x_0\right) \]

根据傅里叶逆变换，我们可以知道：

\[ p_t(x)=\frac{1}{\sqrt{2\pi}}\int \tilde{p}_t(w)e^{iwx}dw \]

同时根据积分恒等式(通过简单的配方即可得到)：

\[ \int e^{-Aw^2}e^{iBw}dw = \sqrt{\frac{\pi}{A}}e^{-\frac{B^2}{4A}} \]

因此,

\[ p_t(w)=\frac{1}{2\pi}\int \exp\left(-\frac{\sigma^2w^2}{4\theta}(1-e^{-2\theta t})\right)\exp\left(-iwe^{-\theta t}x_0\right)e^{iwx}dw \]

那么我们可以令：

\[ A=\frac{\sigma^2}{4\theta}(1-e^{-2\theta t}),\\ B = x-e^{-\theta t}x_0 \]

那么,

\[ p_t(w)=\frac{1}{2\pi}\sqrt{\frac{\pi}{A}}e^{-\frac{B^2}{4A}}=\frac{1}{\sqrt{2\pi2A}}e^{\frac{B^2}{2\times 2A}} \]

我们可以知道$p_t(w)$构成了一个，均值为$e^{-\theta t}x_0$，方差为$\frac{\sigma^2}{2\theta}(1-e^{-2\theta t})$ 的高斯分布。

参考文献

Ho, Jonathan, and Tim Salimans. “Classifier-Free Diffusion Guidance.” arXiv, July 25, 2022. http://arxiv.org/abs/2207.12598.

Lipman, Yaron, Ricky T. Q. Chen, Heli Ben-Hamu, Maximilian Nickel, and Matt Le. “Flow Matching for Generative Modeling.” arXiv, February 8, 2023. https://doi.org/10.48550/arXiv.2210.02747.

Liu, Xingchao, Chengyue Gong, and Qiang Liu. “Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow.” arXiv, September 7, 2022. http://arxiv.org/abs/2209.03003.

Song, Jiaming, Chenlin Meng, and Stefano Ermon. “Denoising Diffusion Implicit Models.” arXiv, October 5, 2022. http://arxiv.org/abs/2010.02502.

Song, Yang, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. “Score-Based Generative Modeling through Stochastic Differential Equations.” arXiv, February 10, 2021. https://doi.org/10.48550/arXiv.2011.13456.

Strümke, Inga, and Helge Langseth. “Lecture Notes in Probabilistic Diffusion Models.” arXiv, December 16, 2023. https://doi.org/10.48550/arXiv.2312.10393.