大模型里的 Attention 机制

引言

近年来，随着深度学习技术的快速发展，大模型（Large Language Models, LLMs）在自然语言处理（NLP）领域取得了显著的进展。这些模型通过大规模数据训练，能够生成高质量的文本、完成复杂的语言理解任务，并在多个领域展现出强大的能力。然而，随着模型规模的不断扩大，如何高效地处理长序列数据、降低计算复杂度以及减少内存占用成为了研究的热点问题。

在大模型中，Attention 机制（注意力机制）是核心组件之一。自 Transformer 模型提出以来，Attention 机制凭借其强大的序列建模能力，逐渐取代了传统的循环神经网络（RNN）和卷积神经网络（CNN）。然而，标准的 Attention 机制（如 Multi-Head Attention, MHA）在处理长序列时面临着计算复杂度和内存占用的双重挑战，这使得其在处理长文本时效率低下。

为了解决这些问题，研究者们提出了多种改进的 Attention 机制，例如 FlashAttention、Multi-Query Attention (MQA)、Group Query Attention (GQA) 以及 Sparse Attention 等。这些方法通过优化计算流程、减少内存访问次数或引入稀疏性，显著提升了 Attention 机制的效率。此外，DeepSeek-V2 提出的 Multi-Head Latent Attention (MLA) 进一步通过低维映射和算子融合技术，降低了计算复杂度和内存占用，为大模型的规模化应用提供了新的思路。

本文将深入探讨这些 Attention 技术的原理、实现细节及其在大模型中的应用。我们将从标准的 MHA 出发，逐步介绍其变体（如 MQA 和 GQA），并详细分析 FlashAttention 如何通过分块计算和重计算技术优化性能。此外，我们还将探讨 Sparse Attention 和 DeepSeek-MLA 的创新设计，以及它们如何在大规模语言模型中实现高效的长序列处理。

通过对这些技术的全面分析，本文旨在为读者提供一个系统的视角，理解大模型中 Attention 机制的演进及其在实际应用中的优化策略。我们相信，随着这些技术的不断发展，大模型将在更多领域展现出其强大的潜力，并为人工智能的未来开辟新的可能性。

Attention 技术

MHA(Multi Head Attention)

Attention is all you need.

Single Head

在基础的 MHA，给定一个 Sequence 的表示\(x\in\mathbb{R}^{N\times d}\)，\(N\)是 Sequence 的长度，\(d\)是表征的维度。

构造三个 Tensor, \(W^Q,W^K,W^V\in\mathbb{R}^{d\times d}\), 那么对应的，

\[ Q=xW^Q, K=xW^K, V=xW^V \]

Attention 的结果\(O\)则变成了：

\(Q=g(QK^T)V\)，这边\(g\)代表按行 softmax 操作。

Multi Head

Single Head 往 Multi Head 的推广则只需要做如下的改变就可以了\(W^Q, W^K, W^V\in\mathbb{R}^{d\times\frac{d}{h}\times h},\)\(h\)是 Head 的个数。下面这段提供了 Multi Head 的 Demo 实现的两种方式：

1. 使用 Single Head 的方式，然后拼接起来
2. 直接完整的张量计算方式

import torch 

batch_size = 8
seq_len = 16
d = 128 
h = 4
sub_d = d // h

x = torch.randn(size=(batch_size, seq_len, d))

w_qs = [torch.randn(size=(d, sub_d)) for _ in range(h)]
w_ks = [torch.randn(size=(d, sub_d)) for _ in range(h)]
w_vs = [torch.randn(size=(d, sub_d)) for _ in range(h)]


print("========From Single Head START=========")
os = []
for head in range(h):
    q = torch.matmul(x, w_qs[head])
    k = torch.matmul(x, w_ks[head])
    v = torch.matmul(x, w_vs[head])
    att = torch.einsum('bnd,bmd->bnm', q, k) / (sub_d ** 0.5)
    att_sep.append(att)
    att = torch.softmax(att, dim=-1)
    att_sep_soft.append(att)
    o = torch.einsum('bnm,bmd->bnd', att, v)
    os.append(o)
output = torch.cat(os, dim=-1)
print("output shape: ", output.shape)
print("========From Single Head END=========")


print("========VEC START=========")
w_qs_vec = torch.stack(w_qs, dim=-1) # (d, sub_d, h)
w_ks_vec = torch.stack(w_ks, dim=-1)
w_vs_vec = torch.stack(w_vs, dim=-1)
q_vec = torch.einsum('bnd,dsh->bnsh', x, w_qs_vec) # (b, n, d, h)
k_vec = torch.einsum('bnd,dsh->bnsh', x, w_ks_vec)
v_vec = torch.einsum('bnd,dsh->bnsh', x, w_vs_vec)
att = torch.einsum('bnsh,bmsh->bnmh', q_vec, k_vec) / (sub_d ** 0.5)
att = torch.softmax(att, dim=-2)
o = torch.einsum('bnmh,bmsh->bnhs', att, v_vec)
output2 = torch.reshape(o, shape=(batch_size, seq_len, d))
print("output2 shape: ", output2.shape)
print("========VEC END=========")


err = torch.sum(torch.abs(output - output2))
print("err: ", err)

上面的具体计算流程可以归纳为如下

从这边我们可以看到传统的 MHA 针对\(N\)的复杂度\(\sim \mathcal{O}(N^2)\)

总体的 FLOPS 可以总结成如下的表格

步骤	Operation	解释	FLOPs(MHA)
1	Q,K,V 的计算	3 个矩阵乘法	\(6Nd^2\)
2	QK^T	\(h\)个矩阵乘法	\(2N^2d\)
3	Softmax	3 来自 exp,求和，除法	\(3N^2h\)
4	乘 V	矩阵乘法	\(2N^2d\)
5	FFN	Dense Layer 的矩阵乘法	\(2Nd^2\)

Flash Attention

Flash Attention：从算法实现的角度，提出了一种IO高效，无损，快速的MHA计算方法。

对于高性能计算程序来说,往往需要从下面两个角度去考虑程序的性能瓶颈:

1. Compute Bottleneck:

   1. 处理器本身的计算能力成了短板。
   2. 在深度学习场景，例如大矩阵的乘法。

2. Memory and IO Bottleneck

   1. 程序大量和内存，显存或者磁盘交互。
   2. 在深度学习场景，各类 element-wise 操作，各类 Reduce 操作。

那么在 MHA 的计算场景，我们从上面的算法中可以看到，整个流程需要频繁写入 HBM，并且立马从 HBM 再次读取的操作，这样往往拖累整个程序的性能。我们简单看一下 GPU 的结构就可以理解为什么会这样。

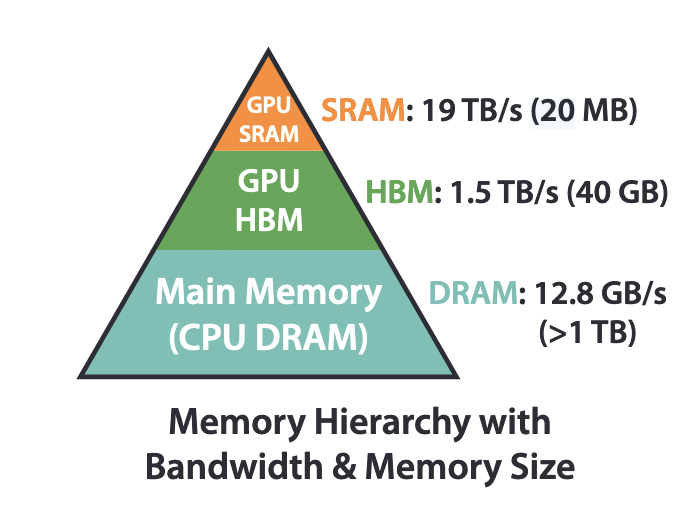
从上面的这张图中，我们可以看到整个 GPU 的内存，分成了三个层次:

1. SRAM: 静态随机存储器，价格昂贵，容量小，但是速度快
2. HBM：即常说的显存
3. CPU DRAM：GPU 机器上的 CPU 的内存

我们可以看到 SRAM 的容量只有 20MB，因此往往不能存储下一个完整的超大 Tensor。在对大矩阵进行计算的时候，会将其分块，并分给不同 CUDA 核心去操作，然后通过 HBM 作为相互通信的中间 Buffer。

所以为了提高传统 MHA 的计算效率，需要遵循下面的原则：

尽可能减少和 HBM 的交互次数，对整个计算做融合(Fuse)

因此在 FlashAttention 的算法中，作者提供了两个模块来完成上述的这件事情：

1. Tiling: 使用分块和流式的方式，降低和 HBM 的交互频率
2. Recomputing: 通过存储 Normalization Factor 的方式，省去了存储超大的中间 Attention Matrix，一样可以保证整体梯度回传的正确性

备注：第二点其实在统计物理中非常常用，一个统计分布的配分函数(partition function),即 Normalization Factor,蕴含了该分布的非常多的信息。

Forward Pass

Tiling 的核心思想就是流式分块计算 softmax。

对于给定一个向量\(x\in\mathbb{R}^{N}\),那么起 softmax 可以按照如下的方式计算：

\[ g(x)_i=\frac{e^{x_i-m(x)}}{\sum_j e^{x_j-m(x)}}, m(x)=\max_i\{x_i\} \]

这边同时减去\(m(x)\)只是从数值稳定性的角度出发。

那么流式分块计算是什么意思，假设我们没有办法一下得到整个\(x\),而是分块得到\(x^{(i)}\),其中\(x=(x^{(1)},x^{(2)},\cdots,x^{(n)}),x^{(i)}\in\mathbb{R}^{d_i},\sum_i d_i = N\)，在这种情况下，我们需要找到一个算法，完美地计算出\(g(x)\)

为了方便讨论，我们考虑最简单的情况，\(x\)被分成了两个 block, \(x^{(1)},x^{(2)}\)。那么整个计算可以按照如下的步骤进行：

1. 当我们拿到第一个 block,\(x^{(1)}\)之后，我们先计算这个 block 本身自己的 softmax，同时保留如下的变量:

   1. \[ m(x^{(1)}),l^{(1)}=\sum_j e^{x^{(1)}_j-m(x^{(1)})} \]
   2. \(g(x)\)的前\(d_1\)个元素更新成\(\frac{e^{x^{(1)}_j}-m(x^{(1)})}{l^{(1)}}\)

2. 当我们拿到第二个 block 的时候，我们知道\(x^{(2)}\)对\(x^{(1)}\)那部分 softmax 值的影响，只有两个方面：

   1. 更新最大值\(m(x)=\max(m(x^{(1)}),m(x^{(2)}))\)，这边\(m(x^{(1)})\)之前所有的最大值，一直通过一个变量维护着，\(m(x^{(2)})\)使用新来的数据\(x^{(2)}\)计算
   2. 更新整体的 normalization factor，\(l(x)=e^{m(x^{(1)})-m(x)}l^{(1)}+e^{m(x^{(2)})-m(x)}l^{(2)}\),这边\(l^{(2)}\)可以使用新来的数据\(x^{(2)}\)临时计算
   3. 更新\(g(x)\),\(g(x)\)前\(d_1\)个元素，可以乘上\(\frac{l^{(1)}}{l(x)}e^{m(x^{(1)})-m(x)}\)这个因子去更新，\(g(x)\)后面新的\(d_2\)个元素，则可以直接赋值\(\frac{e^{x^{(2)}-m(x)}}{l(x)}\)

如果理解清楚上面这个简单的\(x\in\mathbb{R}^{N}\)的情况，那么不能扩展到 Attention 真正面临的场景。

1. 从\(\mathbb{R}^{N}\)求 softmax 扩展到任意\(B_r\)行,\(B_c\)列的矩阵\(\mathbb{R}^{B_r\times B_c}\)的按行求 softmax。

   1. \(l,m\)变成一个\(\mathbb{R}^{B_r}\)的向量，\(g\)变成一个\(\mathbb{R}^{B_r\times B_c}\)的矩阵
   2. \(\frac{1}{l(x)}\)的操作变成矩阵求逆操作

2. Atttention Matrix \(QK^T\)按照硬件参数拆分成个个小的 Block

3. 意识到\(V\)的乘法，只和 Block 本身的位置又关系，softmax 本身的流式更新并不影响。

那么在这种情况下面，我们就会知道在 Forward Pass 过程中，FlashAttention 整体的算法可以表述成下图:

Algorithm 1 \(\mathcal{O}(N^2d)\) FLOPs and requires \(\mathcal{O}(N)\) additional memory beyond inputs and output.

FLOPS 主要来自于\(Q_iK_j^T\)的矩阵乘法: \(T_c T_r B_rB_cd \sim \mathcal{O}(N^2d)\)

额外的\(\mathcal{O}(N)\)的显存开销来自于\(l,m\)向量的存储

标准MHA需要和HBM交互\(\mathcal{O}(Nd+N^2)\)次，FlashAttention需要和HBM交互\(\mathcal{O}(N^2d^2M^{-1})\)次

标准 MHA Load \(Q,K,V\)需要\(\mathcal{O}(Nd)\), Attention Matrix 的读写需要\(\mathcal{O}(N^2)\)

FlashAttention 主要 Load \(T_r T_c\)次\(M\)大小量级的 Tensor, 因此\(T_rT_cM \sim \mathcal{O}(N^2d^2M^{-1})\)

在一般情况下面\(M\gg d^2\),因此 FlashAttention 的交互次数会被大幅度压缩。

当然在 LLM 的训练过程中，因为有 Sequence Mask 的存在，往往很多 Attention Block 不需要计算，可以直接认为是一个\(-\infty\)，因此作者证明了，对于 Sparse 结构的 Attention，整体与 HBM 交互次数可以压缩到\(\mathcal{O}(N^2d^2M^{-1}s)\),\(s\)用来很衡量稀疏度。

Backward Pass

在分析完了 Forward Pass 之后，我们需要证明：

维护\(Q,K,V,l\)就足够完成梯度计算，不需要维护中间的Attention Matrix\(P:=g(QK^T)\)

假设梯度回传到\(O\)的时候为\(O^{\prime} \in \mathbb{R}^{N\times d}\), 因为\(O=PV\)，根据链式法则我们可以有:

\(V'_{ij} = \frac{\partial O_{rs}}{\partial V_{ij}} O'_{rs}=P_{ri}\delta_{sj}O'_{rs}=P^T_{ir}O'_{rj}=\sum_r\frac{e^{q_rk_i^T}}{l_r}O'_{rj}\)，即\(V'=P^TO'\).

因为关于\(V\)的梯度，可以仿照从 V 到 O 的过程，使用类似 ForwardPass 的方式进行计算从\(O'\)到\(V'\).

下面我们还需要确认一下\(Q',K'\)是不是也可以比较方便的计算出来。根据\(O=PV\),我们可以类似的得到\(P'=O'V^T\),即我们可以用上面的方式计算出来\(P'\)。

\[ Q'_{i,:}=P'_{is}\frac{\partial P_{is}}{\partial Q_{i:}}=P'_{is}\frac{\partial P_{is}}{\partial S_{it}}\frac{\partial S_{it}}{\partial Q_{i:}}=(\delta_{st}P_{is}-P_{is}P_{it})P'_{is}K_{t:}=\sum_tP_{it}(O'_{i:}V_{j:}-O'_{i:}O_{i:})K_{t:} \]

V2

FlashAttention-V2 的版本在 V1 的基础上做了一些小的优化:

1. 原来在更新O的过程中，每一步都是用老的\(l_{old}\)和新的\(l_{new}\)去做scale，将整个softmax计算结果保持到根据已有数据能算到最准确的结果。但是实际过程中，我们只关心最终结果的准确性，所以中间过程，完全不需要去对O做scale，只需要不断维护最新的\(l\),等到计算结束之后统计做scale
2. 在反向过程中不需要维护完整的\(m\)\(和\)\(l\)，只需要维护\(L=m+\log l\)，但是感觉这边本身的消耗就应该很小？

算法的核心改动就是红色圈出来的两部分。

V3

针对 Hopper GPU，例如 H100 的优化

MQA(Multi Query Attention)

MQA 算法，是对 MHA 一种近似替代，正如上面看到的，在 MHA 中,\(W^Q, W^K, W^V\in\mathbb{R}^{d\times\frac{d}{h}\times h},\)MQA 则是对于\(W^K,W^V\)做了共享的优化，所有的 head 共享相同的参数，变成\(W^K,W^V\in\mathbb{R}^{d\times\frac{d}{h}}\)，以此来降低整个算法的计算复杂度。

GQA(Group Query Attention)

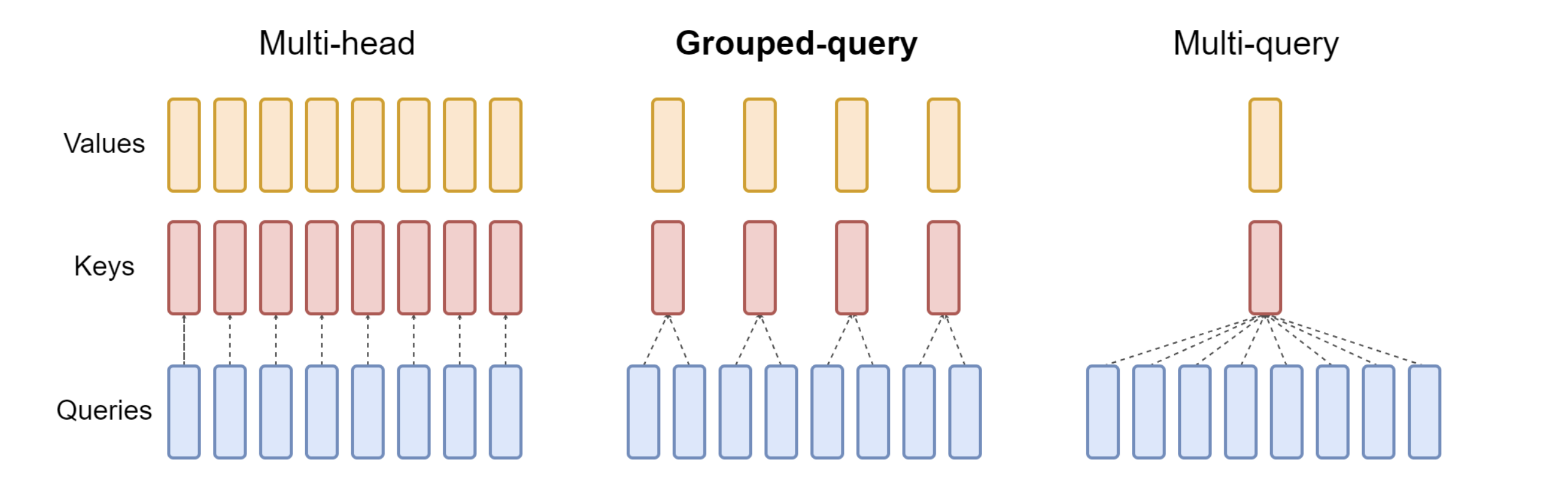
MQA 相比于 MHA 跨度过大，在很多实验中，模型性能下降很明显，因此后续研究者，有提出来一个鉴于 MHA 和 MQA 中的方法，Key 和 Value 从不同 head 之间完全独立和完全共享，选择了一种分组共享的折中方式，以此平衡整个效率和性能。

如果我们\(h\)个 head 分成了\(h_g\)个 Group，我们可以看看整体 FLOPS 减少到多少。首先对比这个表格大模型里的 Attention 机制，我们可以发现，GQA 只是降低了第一步的 FLOPS，

\[ 6Nd^2 \to 2Nd^2+4Nd^2\frac{h_g}{h} \]

不过在 GQA 的文章中，作者提出来一个 Uptraining 的思路，做法很简单，不过开辟了从基于 MHA 训练得到 checkpoints 之后可以自由切换到 MQA 或者 GQA 去进行 finetuning，这样就可以极大可能的保证性能和效率。

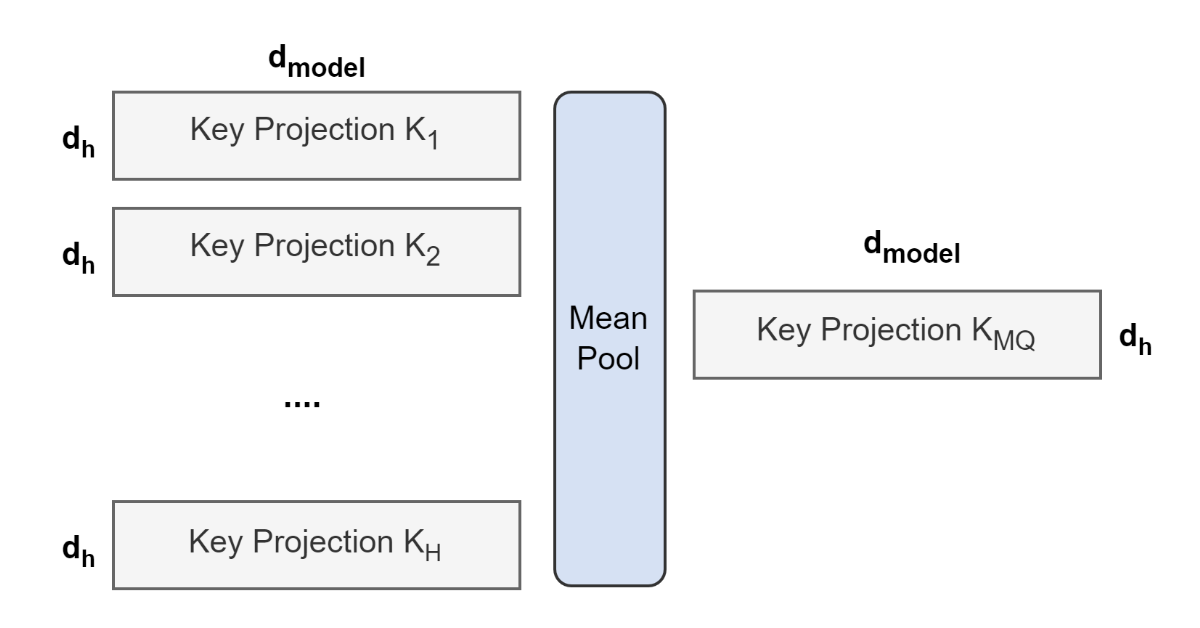
做法就是很简单的对于基于 MHA 训练好的 chekpoints 的\(W^K,W^V\)做分组然后去平均。

Sparse Attention

SWA(Sliding Window Attention)

SWA(Sliding Window Attention),该方法是一种“倒退”的想法。我们知道在 CNN 类型的结构中，每个卷积操作都是 Local 信息的融合，需要不断加深网络的深度，才能慢慢捕捉 Global 的信息。

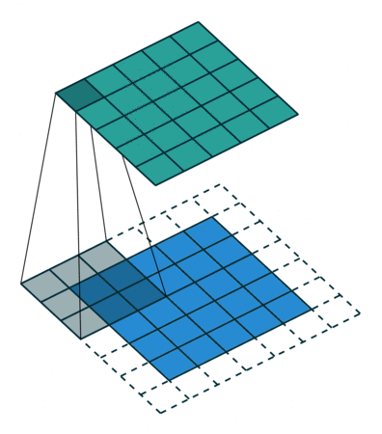
VisionTransformer 的提出，则是想借助 Attention 这种全局的机制，去直接捕获 Global 的信息。

SWA 则是觉得全局 Attention 的机制计算复杂度太高，通过使用 Mask 的方式，将每层的 Attention 限制在局部。

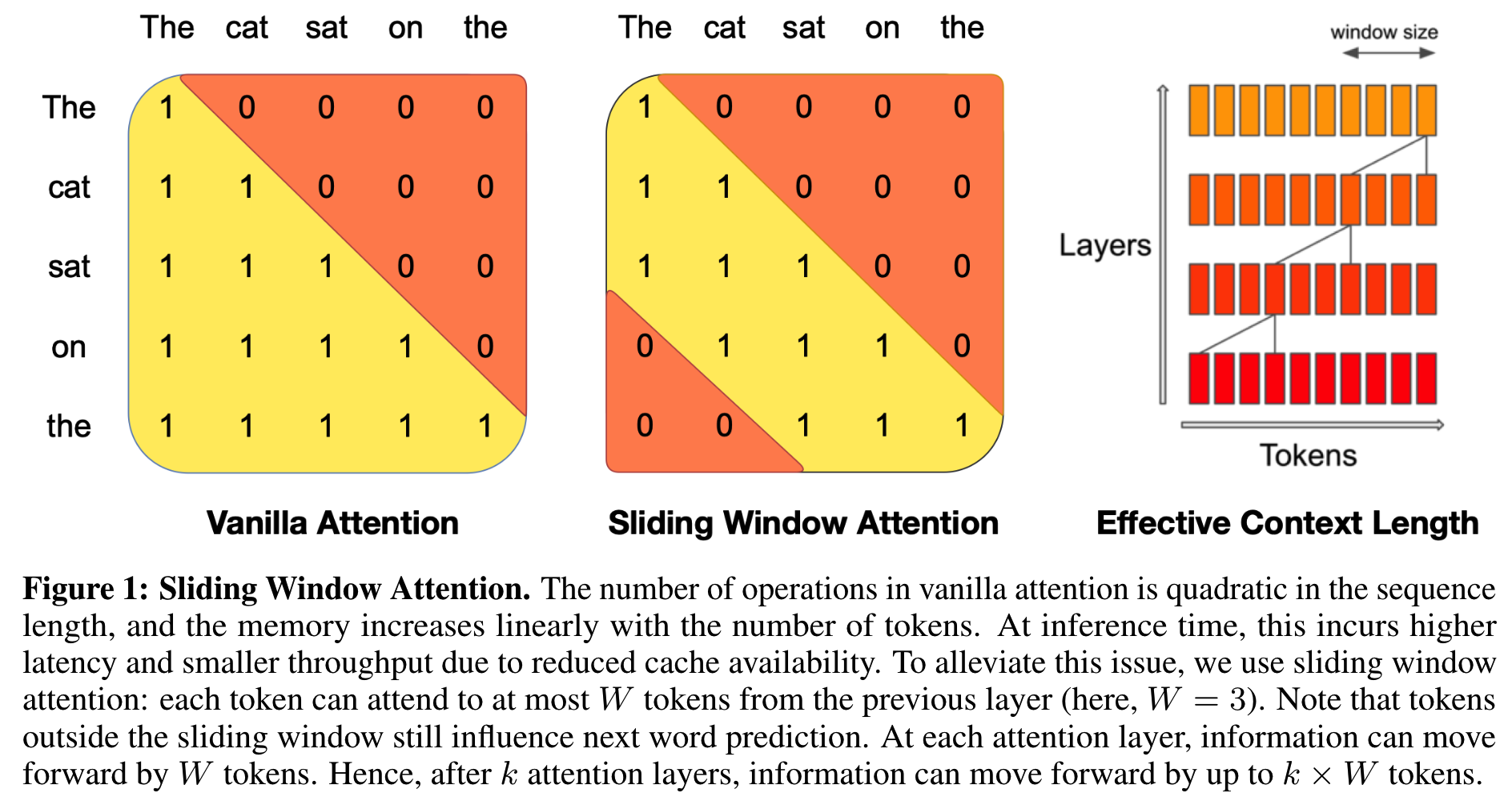
最左边则是正常的 Attention 对应的 Casual Mask，是一个下三角矩阵。中间则是 SWA 限制了 Attention 范围的 Mask 矩阵，最右边则是 SWA 通过深度不断加深之后，整体个模型视野图。

从上面这个图上，我们可以看到 SWA 带来的好处有下面两个点：

1. 从 FLOPS 的角度来说，MHA 计算中很多\(\mathcal{O}(N^2)\)的操作，都不会随着\(N\)再以平方的速度增长。
2. 从 KV Cache 的角度来说，当超过 Window 长度的 KV 就不再需要缓存，大幅度节省了 Cache。

LongFormer

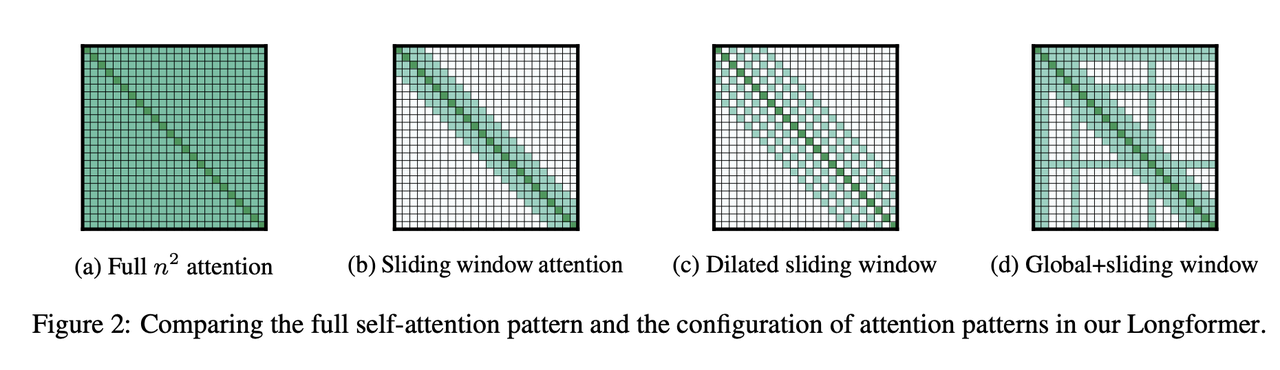
和 SWA 这种借鉴 CNN 思想的 Attention 机制，后面又有一些类似的 Sparse Attention 机制被提出来，总体结构和下面的图类似。

Deepseek-MLA(MultiHead Latent Attention)

MLA 原理

Deepseek-V2 在技术报告中提出来他们的 MLA 技术，主要以此来降低整个 KV Cache 的消耗，同时降低 FLOPS。

从上面我们知道，在原始的 MHA 中，所有的\(Q,K,V\)都来自于上一层的输出表示\(\mathbb{R}^d\), 同时 KV Cache 也需要 Cache \(\mathcal{O}(2Nd)\)。在 MLA 当中，作者采用了类似 LORA 的一些做法，先将\(x\in\mathbb{R}^d\)映射到一个低维的空间，

\[ \begin{gather} c^{KV}=xW_{D}^{KV}, c^Q=xW_{D}^{Q}\\ W_{D}^{KV}\in\mathbb{R}^{d\times d_c^{KV}}, W_{D}^{Q}\in \mathbb{R}^{d\times d_{c}^Q}\\ d_c^{KV},d_c^{Q} \ll d \end{gather} \]

那么这个时候，所有的\(K,V\)都是基于这个共有的\(c\)再升维上去，即：

\[ \begin{gather} k=c^{KV}W_{U}^{K},v=c^{KV}W_{U}^{V},W_{U}^{K}, q=c^QW_{U}^Q\\ W_{U}^V \in \mathbb{R}^{d_c^{KV}\times d}, W_{U}^Q\in \mathbb{R}^{d_c^Q \times d} \end{gather} \]

那我们分别从 FLOPS 和 KV Cache 的角度来看这么做的好处：

1. FLOPS: 对于\(Q,K,V\)的计算的需要的 FLOPS 从 \(6Nd^2\)变成了\(6Ndd_c^{KV}+4Ndd_c^Q\)，而\(d_c^{KV},d_c^{Q} \ll d\)，因此 FLOPS 的得到了大幅度减少。
2. KVCache: 原始 MHA 的 KV Cache 每层需要 \(2Nd\)，MLA的KV Cache只需要\(Nd_c^{KV}\) 因此也大幅度减少了。

那么当然第一个疑问是不是如果我们只缓存\(c^{KV}\)，那么在推理的时候，我们仍然需要实时去计算\(c^{KV}W_U^K, c^{KV}W_U^V\)这两个矩阵乘法，那么 MLA 是不是一种以时间换取空间的策略呢？

当然，这边作者们发现在推理阶段，可以对模型算子做融合，从而避免上面的计算开销。我们以\(qk^T\)的计算为例，看看如何进行融合掉\(W_U^K\)。

\[ qk^T=c^QW_U^Q(W_U^K)^T(c^{KV})^T:=c^QW_U^{QK}(c^{KV})^T \]

因此，我们可以将\(W_U^K\)融入到\(W_U^Q\)当中去。类似的，我们也可以将\(W_U^V\)融合到\(W^O\)，即 Attention 的 FFN 的权重当中去，避免重复计算。

因此在推理阶段，如果考虑算子的融合 FLOPS 会进一步从 \(6Ndd_c^{KV}+4Ndd_c^Q\)压缩到\(2N(dd_c^{KV}+dd_c^Q+d_c^Qd_c^{KV})\)

MLA 的 RoPE

我们知道在 Transformer 架构中，都会加入 Position Encoding 来让模型感知到每个 Token 在时间序列中所处的位置。当然，对于 Position Encoding 的也有很多讨论，不过现在的主流 LLM 都几乎使用 RoPE，这边我们就简单介绍一下 RoPE 的原理。

在笔者看来，RoPE 的特点可以总结成如下的一句话：

RoPE 寻求一种绝对位置的 PE 表示方法，但是又可以保证在计算\(qk^T\)的时候能保持相对位置的一致性。

而\(qk^T\)作为一种内积的计算，满足上面的要求的表示，很显然就是旋转矩阵。因此，对于传统的 MHA，我们则可以乘上一个旋转矩阵,

\[ q_i^R=q_iR(i,\theta),k_j^R=k_jR(j,\theta) \]

这边\(i,j\)代表的是第\(i,j\)个 token。那么，

\[ q_i^R(k_j^R)^T=q_iR(i,\theta)R^T(j,\theta)k_j^T=q_iR(i-j,\theta)k_j^T \]

保证了相对位置的一致性。

那么如果我们直接将这种方式从 MHA 推广到 MLA，会遇到怎么样的问题呢？

\[ q_i^R(k_j^R)^T=c_i^QW_U^QR(i,\theta)R^T(j,\theta)(W_U^K)^T(c_j^{KV})^T \]

从上面的表达式，我们可以看到两个旋转矩阵\(R(i,\theta),R(j,\theta)\)插在了两个\(W\)中间，而这两个旋转矩阵又和绝对的位置\(i,j\)有关系，因此我们就没有办法去做算子融合，这就让 MLA 在推理阶段的性能优势大幅度降低。

那么在 Deepseek 的 V2 中，采取了一种折中的处理方式，值得注意的是，Deepseek 处理方式其实是在一定程度上，破坏了 RoPE 的设计理念的，即：

DeepSeek-MLA-RoPE 是不能保持相对位置的一致性的。

Deepseek 额外引入了\(q^R,k^R\)使用 RoPE 编码位置信息，即:

\[ q^R:=\mathrm{RoPE}\left(c^QW^{QR}\right),k^R:=\mathrm{RoPE}\left(xW^{KR}\right),W^{QR}\in\mathbb{R}^{d_c^Q\times d_R}, W^{KR}\in\mathbb{R}^{d\times d_R} \]

然后使用了暴力拼接的方法得到了\(q,k\):

\[ q\leftarrow [q, q^R], k \leftarrow [k, k^R] \]

参考文献

Ainslie, Joshua, James Lee-Thorp, Michiel de Jong, Yury Zemlyanskiy, Federico Lebrón, and Sumit Sanghai. “GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints.” arXiv, December 23, 2023. https://doi.org/10.48550/arXiv.2305.13245.

Beltagy, Iz, Matthew E. Peters, and Arman Cohan. “Longformer: The Long-Document Transformer.” arXiv, December 2, 2020. https://doi.org/10.48550/arXiv.2004.05150.

Dao, Tri, Daniel Y. Fu, Stefano Ermon, Atri Rudra, and Christopher Ré. “FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness.” arXiv, June 23, 2022. https://doi.org/10.48550/arXiv.2205.14135.

Lu, Enzhe, Zhejun Jiang, Jingyuan Liu, Yulun Du, Tao Jiang, Chao Hong, Shaowei Liu, et al. “MOBA: MIXTURE OF BLOCK ATTENTION FOR LONG-CONTEXT LLMS,” n.d.

Shah, Jay, Ganesh Bikshandi, Ying Zhang, Vijay Thakkar, Pradeep Ramani, and Tri Dao. “FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-Precision.” arXiv, July 12, 2024. https://doi.org/10.48550/arXiv.2407.08608.

Shazeer, Noam. “Fast Transformer Decoding: One Write-Head Is All You Need.” arXiv, November 5, 2019. http://arxiv.org/abs/1911.02150.

Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. “Attention Is All You Need.” arXiv, August 2, 2023. https://doi.org/10.48550/arXiv.1706.03762.

Yuan, Jingyang, Huazuo Gao, Damai Dai, Junyu Luo, Liang Zhao, Zhengyan Zhang, Zhenda Xie, et al. “Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention.” arXiv, February 16, 2025. https://doi.org/10.48550/arXiv.2502.11089.

DeepSeek-AI, Aixin Liu, Bei Feng, Bin Wang, Bingxuan Wang, Bo Liu, Chenggang Zhao, et al. “DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model.” arXiv, June 19, 2024. http://arxiv.org/abs/2405.04434.

DeepSeek-AI, Aixin Liu, Bei Feng, Bing Xue, Bingxuan Wang, Bochao Wu, Chengda Lu, et al. “DeepSeek-V3 Technical Report.” arXiv, December 27, 2024. https://doi.org/10.48550/arXiv.2412.19437.

Touvron, Hugo, Louis Martin, and Kevin Stone. “Llama 2: Open Foundation and Fine-Tuned Chat Models,” n.d.