Position Based Dynamics

🖌 PBD 这一类物理模拟方法，不同于基于经典力学那套方法，写出动力学方程，然后数值求解 PDE 的范式。而是直接只考虑外力作用，将内力全部归结于不同的约束条件考虑。使用投影的方法去解决外力作用更新之后的约束之间的冲突问题。

Basic info

PBD 相关的物理模拟方法

• Author: anschen

• Reading cycle

  • Start date 2024/05/23
  • End date 2024/06/10

Notations

---

三维空间的向量 对时间求全导数

\[ \mathbf{x} \]

\[ \dot{x} \]

---

Position Based Dynamics

在这个章节，我们将主要介绍原始的 PBD 算法的细节和原理，从而构建一个完整的 PBD 这套方法论的大框架。

Model

我们考虑如下建模场景，对于一个物体，有\(N\)个顶点， \(M\)个约束条件，每个顶点的质量，位置，速度分别为\(m_i,\mathbf{x}_i,\mathbf{v}_i\)。这边的约束条件可以按照如下的语言描述：

1. A cardinality \(n_j\)
2. A function \(C_j:\mathbb{R}^{3n_j} \to \mathbb{R}\)
3. A set of indices \(\{i_1, \cdots, i_{n_j}\}, i_k \in [1, \cdots, N]\)
4. A stiffness parameter \(k_j \in [0, 1]\)
5. A type of equality or inequality , i.e. \(C_j(\mathbf{x}_{i_1}, \cdots, \mathbf{x}_{i_{n_j}}) = 0;\)or \(C_j(\mathbf{x}_{i_1}, \cdots, \mathbf{x}_{i_{n_j}}) \ge 0\)

Algorithm

算法总结：

1. 第 5 步，只考虑外力的作用，相对简单。
2. 第 7-8 两步，使用临时的位置去生成新的碰撞约束。
3. 第 9-11 步，则是整个算法的核心，如何通过投影的方式来解决整个约束之间的冲突关系。
4. 第 12-16 步，则通过使用解决完冲突之后的位置，计算速度，以此保证整个过程的一致性。

Constraint Projection

在这个小节，我们将详细介绍如何通过迭代投影的方法去解决约束问题。

首先在经过算法第 5-6 步之后，外力对系统的影响，已经被归纳进入临时的位置\(\mathbf{p}_i\)，那么在约束投影这一步，我们需要我们的系统满足下面两条物理定律（下面的两个方程都忽略了固定时间间隔\(\Delta t\)）：

1. 动量守恒 \(\sum_i m_i \Delta \mathbf{p}_i = 0\)
2. 角动量守恒 \(\sum_i \mathbf{r}_i \times m_i \Delta\mathbf{p}_i = 0\)，其中\(\mathbf{r}_i\)为\(\mathbf{p}_i\)到任意旋转中心的矢量。

对于刚体系统，我们知道任意的约束\(C(\mathbf{p}), \mathbf{p}=(\mathbf{p}_1^T, \cdots, \mathbf{p}_n^T)^T\)都应该满足平移不变性和旋转不变性。因此，这边我们可以借鉴经典力学中的诺特定理[https://en.wikipedia.org/wiki/Noether%27s_theorem]的推导方式，得出如下重要的结论。

NOTE 如果所有顶点的质量\(m_i\)都相等，那么沿着\(\nabla_{\mathbf{p}}C(\mathbf{p})\)更新\(\Delta\mathbf{p}\)，更新后的系统自动满足动量守恒和角动量守恒。

证明分为两部分：动量守恒和角动量守恒

动量守恒

\[ C(\mathbf{p}+\Delta\mathbf{p}) = C(\mathbf{p}) + \nabla_{\mathbf{p}}C(\mathbf{p})\Delta\mathbf{p}+o(\Delta\mathbf{p}^2) \]

如果\(\Delta\mathbf{p}_i = \delta\mathbf{r}, \forall i \in [1, n] \)，即所有顶点平移一个相同的无限小位移\(\delta\mathbf{r}\)，那么平移不变性要求如下的方程成立:

\[ \sum_i \nabla_{\mathbf{p}_i}C(\mathbf{p})\delta\mathbf{r} = 0, \forall \delta\mathbf{r} \]

因此，如果\(m_i = m\)，我们可以得到动量守恒：\(0 = m\sum_i\nabla_{\mathbf{p}_i}C(p) = \sum_im_i \nabla_{\mathbf{p}_i}C(p)\)

角动量守恒

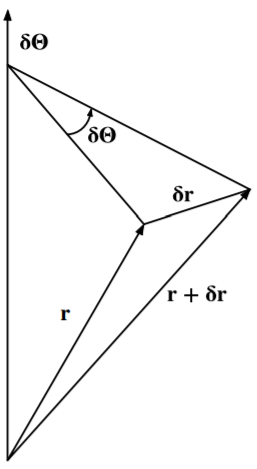
对于旋转不变性，我们可以仿照平移不变性，对\(C(\mathbf{p})\)施加一个类似的无穷小旋转变换，如上图所示。那么这个时候，无穷小旋转变化的对应的偏移矢量\(\delta\mathbf{r}=\delta\mathbf{\Theta} \times \mathbf{r}\)，因此

\[ \sum_i \nabla_{\mathbf{p}_i}C(\mathbf{p}) \delta\mathbf{\Theta} \times \mathbf{r}_i = \delta\mathbf{\Theta} \cdot\sum_i \mathbf{r}_i \times \nabla_{\mathbf{p}_i}C(\mathbf{p}) = 0, \forall \delta\mathbf{\Theta} \]

因此，如果\(m_i = m\)，我们可以得到动量守恒：\(0 = m \sum_i \mathbf{r}_i \times \nabla_{\mathbf{p}_i}C(\mathbf{p}) = \sum_i \mathbf{r}_i \times m_i\nabla_{\mathbf{p}_i}C(\mathbf{p})\)

更新尺度

在我们确定了\(\Delta\mathbf{p}\)的更新方向之后，接下来确定更新的步幅则可以完成整个更新工作，最起码对于质量是一样的情况是这样。考虑 equality 类型的约束，即\(C(\mathbf{p}+\Delta\mathbf{p})=0, \Delta\mathbf{p}=\lambda \nabla_{\mathbf{p}}C(p)\)，我们可以容易求解出来：

\[ \lambda = -\frac{C(\mathbf{p})}{\|\nabla_\mathbf{p}C(\mathbf{p})\|^2} \]

不同质量

在上面的讨论中，我们完整了讨论了，如果质量是相同情况，投影更新规则。但是如果质量各不相同，则上面所说的动量和角动量守恒则会被破坏。以动量守恒为例，平移不变性只能得到\(\sum_i\nabla_{\mathbf{p}_i}C(p)=0\)，那么这个时候如果我们仍然要求\(\sum_im_i \Delta\mathbf{p}_i = 0，\Delta\mathbf{p}_i = \lambda_i \nabla_{\mathbf{p}_i}C(\mathbf{p})\)，一个比较好的处理方式：根据各个顶点的质量\(m_i\)去调整更新的步幅\(\lambda_i\)。

\[ \lambda_i = -\frac{w_i C(\mathbf{p})}{\sum_i w_i \|\nabla_{\mathbf{p_i}}C(\mathbf{p})\|^2},w_i=\frac{1}{m_i} \]

对于这样的更新法则，可以同时保证三件事：

1. 动量守恒
2. 角动量守恒
3. \(C(\mathbf{p}+\Delta\mathbf{p})=0\)

Inequality 约束条件

上面的讨论都是针对了 Equality 类型的约束条件进行的，即\(C(\mathbf{p}+\Delta\mathbf{p})=0\)，对于 Inequality 类型的约束条件，我们则可以比较好的处理，因为\(\nabla_{\mathbf{p}_i}C(\mathbf{p})\)代表\(C(\mathbf{p})\)增加最快的方向，那么如果我们的要求是\(C(\mathbf{p}+\Delta\mathbf{p})\ge 0\)，我们则可以选择只对那些约束条件还小于 0 的约束进行投影更新。

Stiffness

刚度(Stiffness)是指物体抵抗形变的能力。在物理模拟中，刚度决定了物体在受到外力作用时的形变程度。

• 高刚度：如果一个物体或系统的刚度很高，这意味着它不容易形变。在模拟中，高刚度的物体在受到力的作用时会表现出较小的形变，这会使得物体看起来更硬或更紧绷。例如，一根硬木棍在受力时几乎不会弯曲。

• 低刚度：相反，低刚度的物体在受力时会表现出较大的形变，这使得物体看起来更软或更容易弯曲。例如，一根橡皮筋在拉伸时会明显延长。 因此，Stiffness 对于整个模拟的影响，可以直接作用到位移\(\Delta\mathbf{p}\)上面，即\(\Delta\mathbf{p} \leftarrow k\Delta\mathbf{p}\)，但是因为我们整个 Constraint Projection 是一个迭代过程，因此最终的 Stiffness 的影响，变成了非线性的。当然在 PBD 原文中，提出来用\((1-k_s)^{n_{iter}}:=1- k\)求解出来的\(k_s\)作为每个迭代步骤中 Stiffness 产生的影响。不过个人对于这个做法并不是特别的赞同：

  1. \(n_{iter}\)对于不同的模拟和物体，为了保证模拟的精度，是一个可变的量。
  2. \((1-k_s)^{n_{iter}}:=1- k\)的由来，是作者认为误差项为\((1-k)^{n_{iter}}\)，对于该结论持保守观点。

个人观点：原始的 PBD，并不能很好地处理 Stiffness 对于整个模拟的影响，尤其是“物理”意义上的正确处理这个过程。

Collision-碰撞

对于碰撞来说，一般需要考虑的碰撞情形，可以简单分成两大类：

1. 和静态物体的碰撞
2. 和动态物体的碰撞

静态碰撞

静态约束碰撞即检测被模拟对象和周围环境中静态障碍物之间的碰撞情况。这个过程可以简单抽象成如下的检测：

如果和静态障碍发生碰撞，则在模拟过程\(\mathbf{x}_i \to \mathbf{p}_i\)的更新穿过穿过某个法向量为\(\mathbf{n}_s\) 表面，因此该约束的数学表示为: \(C(\mathbf{p}_i) = (\mathbf{p}_i - \mathbf{p}_s) \cdot \mathbf{n}_s \ge 0\)，其中\(\mathbf{p}_s\)为射线\(\mathbf{x}_i \to \mathbf{p}_i\)和面的投影。

动态碰撞

所谓动态碰撞，即被模拟对象之间发生了碰撞。这个过程可以用如下的语言描述:

假设一个物体的顶点\(\mathbf{q} \to \mathbf{p}\)，与另外一个物体发生了碰撞，则另外一个物体存在一个三角面其顶点为\(\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3\)被穿过，其数学表示为: \(C(\mathbf{p},\mathbf{q},\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3) := \pm (\mathbf{p}-\mathbf{q})\cdot ((\mathbf{p}_1-\mathbf{p}_2)\times(\mathbf{p}_1-\mathbf{p_3})) \ge 0\)，这边\(\pm \)取决于最终法向朝向表面的那一侧。

Damping

Damping 是指抵抗运动的力，它消耗掉系统的能量。在物理模拟中，阻尼用于模拟那些减缓运动和振动的效果。

• 高阻尼：高阻尼意味着运动能量会快速消耗，导致物体的运动或振动很快减弱直至停止。这在模拟如防震器或是其他需要快速平息振动的场景时非常有用。
• 低阻尼：低阻尼意味着运动能量消耗得慢，物体的运动或振动会持续较长时间。这可以用来模拟如弹簧振动等持续较长时间的动态效果。

在动力学模拟中，适当的阻尼可以防止系统过度振动或“爆炸”，帮助保持模拟的稳定性和真实性。

比较简单来描述 Damping 的方式，可以用下面的算法:

其中\(\tilde{\mathbf{r}}_i \in \mathbb{R}^{3\times 3}, \tilde{\mathbf{r}}_i \mathbf{v} = \mathbf{r}_i\times\mathbf{v} \)。那么对于两种极限的高低阻尼情况:

1. \(k_{damping} = 0\) 整个过程保证完全没有阻尼，没有阻尼这部分的更新
2. \(k_{damping}=1\) 整个过程，所有顶点的速度，都为质心平移速度加上顶点的转动速度，整个模式表现为刚体模式。

从上面的算法中我们也可以看出来，阻尼只是在限制局部的运动，整体的运动并不受影响。

XPBD

通过对 PBD 的介绍吗，我们可以知道 PBD 的拥有简洁的算法逻辑，但是正如前面我们提到的，PBD 至少存在如下几个方面的问题：

1. PBD 总体上是一个 explicit 的算法，因此非常依赖\(\Delta t\)是一个非常小的值，因此需要较长的步数
2. PBD 对于 stiffness 的处理，缺乏较强的物理依据，同时还是依赖于不确定的参数 \(n_{iter}\)

XPBD 的提出，则是为了缓解上面两个问题带来的模拟效果退化。

XPBD 的总体思路，回归了原始的牛顿力学，即将约束重构成势能，去求解经典力学的方程。在 PBD 中，约束只是作为等式或者不等式的数学条件存在，在每次模拟过程中，通过数学更新去让新的位置满足对应的约束条件，当然这个过程中保证了一些的物理规律，例如动量守恒，角动量守恒等等。但是正如上面所说，还是存在很多没有那么物理的地方。

经典力学离散化

在迭代过程中，位置的信息用如下的序列表示\(\mathbf{x}^1, \cdots, \mathbf{x}^i, \mathbf{x}^{i+1},\cdots\)，那么牛顿第二定律可以很简单地写成如下形式:

\[ \mathbf{M}\frac{\mathbf{x}^{i+1}-2\mathbf{x}^i+\mathbf{x}^{i-1}}{\Delta t^2}=-\nabla U(\mathbf{x}^{i+1}) \]

值得注意的是，在方程的右侧我们使用了\(U(\mathbf{x}^{i+1})\)而非\(U(\mathbf{x}^i)\)，以保证整个过程是一个 implicit 的过程，来缓解对\(\Delta t\)要求很小的严苛条件。当然这边的势能\(U(\mathbf{x})\)是用来描述约束条件的，可以表示成如下形式：

\(U(\mathbf{x}) = \frac{1}{2}C^T(\mathbf{x}) \boldsymbol{\alpha}^{-1} C(\mathbf{x})\)，

其中是一个对角矩阵，用来描述 stffiness 强度的倒数，即所谓的 compliant matrix. 因此，

\[ \mathbf{M}(\mathbf{x}^{i+1}-2\mathbf{x}^i+\mathbf{x}^{i-1})=-\nabla C^T(\mathbf{x}^{i+1})\boldsymbol{\alpha}^{-1}C(\mathbf{x}^{i+1})\Delta t^2 := \nabla C^T(\mathbf{x}^{i+1}) \boldsymbol{\lambda}^{i+1} \]

在上面的方程中\(\boldsymbol{\lambda}:=-\tilde{\boldsymbol{\alpha}}^{-1}C(\mathbf{x})\)，\(\mathbf{x}^{i+1}, \boldsymbol{\lambda}^{i+1}\)为需要求解的变量。同时我们知道\(\tilde{\mathbf{x}}^i:=2\mathbf{x}^{i}-\mathbf{x}^{i-1}=\mathbf{x}^i+\mathbf{v}^i\Delta t\)。最终需要求解的方程组为如下：

\[ \mathbf{M}(\mathbf{x}-\tilde{\mathbf{x}})-\nabla C^T(\mathbf{x})\boldsymbol{\lambda} = 0 \\ C(\mathbf{x})+\tilde{\boldsymbol{\alpha}}\boldsymbol{\lambda} = 0 \]

其中\(\tilde{\boldsymbol{\alpha}} = \frac{\boldsymbol{\alpha}}{\Delta t^2}\)，同时省略了上标。对于如何求解上面的方程有很多的方法， 这边采用最简单原始的方法，即牛顿迭代法[https://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95], 因此我们直接线性化上面的方程：

\[ \left[\begin{array}{cc}\mathbf{M} - (\nabla\nabla^T) C^T(\mathbf{x}^i) \boldsymbol{\lambda}^i & -\nabla C^T(\mathbf{x}^i) \\ \nabla C(\mathbf{x}^i) & \tilde{\boldsymbol{\alpha}}\end{array}\right]\left[\begin{array}{c}\Delta\mathbf{x}\\ \Delta\boldsymbol{\lambda}\end{array}\right]=-\left[\begin{array}{c}\mathbf{M}(\mathbf{x}^i-\tilde{\mathbf{x}})-\nabla C^T(\mathbf{x}^i)\boldsymbol{\lambda}^i \\ C(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}}\boldsymbol{\lambda}^i \end{array}\right] \]

XPBD 在处理上面的方程，为了更加容易求解，引入了如下两个假设： - \[(\nabla\nabla^T) C^T(\mathbf{x}^i) \boldsymbol{\lambda}^i \approx 0\] - \[\mathbf{M}(\mathbf{x}^i-\tilde{\mathbf{x}})-\nabla C^T(\mathbf{x}^i)\boldsymbol{\lambda}^i \approx 0\]

对于被忽略的两项，我们可以知道误差都在\(o(\Delta t^2)\)这个量级上。同时整个方程被简化成：

\[ \left[\begin{array}{cc}M & -\nabla C^T(\mathbf{x}^i) \\ \nabla C(\mathbf{x}^i) & \tilde{\boldsymbol{\alpha}}\end{array}\right]\left[\begin{array}{c}\Delta\mathbf{x}\\ \Delta\boldsymbol{\lambda}\end{array}\right]=-\left[\begin{array}{c} 0 \\ C(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}}\boldsymbol{\lambda}^i \end{array}\right] \]

使用 Shur Complement[https://en.wikipedia.org/wiki/Schur_complement] 我们可以轻松解出上面的方程:

\[ \Delta\mathbf{x}=\mathbf{M}^{-1}\nabla C^T(\mathbf{x}^i)\Delta\boldsymbol{\lambda}\\ \Delta\boldsymbol{\lambda}=(\nabla C(\mathbf{x}^i)\mathbf{M}^{-1}\nabla C^T(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}})^{-1}(C(\mathbf{x}^i+\tilde{\boldsymbol{\alpha}}\boldsymbol{\lambda}^i)) \]

Connection with PBD

上面直接给出来了\(\Delta\mathbf{x},\Delta\boldsymbol{\lambda}\)的解析更新公式。但是实际使用时，直接对矩阵求逆不是一个很好的操作，更多的时候会采用一些其他的算法来求解线性方程组，例如经典的 Gauss-Seidel 算法。

然而，在原始论文里，作者直接得出了如下的结论:

\[ \Delta\boldsymbol{\lambda}_j=\frac{-C_j(\mathbf{x}^i)-\tilde{\boldsymbol{\alpha}}_j\boldsymbol{\lambda}_j^i}{\nabla C_j(\mathbf{x}^i)M^{-1}\nabla C_j^T(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}}_j}` \]

这边是十分不理解为什么可以讲不同约束之间的相互影响给独立处理。

当然这边如果处理完毕之后，我们会发现在\(\tilde{\boldsymbol{\alpha}}_j=0\)的情况下面，整个过程退化到 PBD 的场景了。

Damping

XPBD 中使用了 Rayleigh dissipation potential 来处理能量耗散的问题：

\[ D(\mathbf{x}):=\frac{1}{2}\dot{C}^T(\mathbf{x})\boldsymbol{\beta}\dot{C}(\mathbf{x})=\frac{1}{2}\mathbf{v}^T\nabla C^T(\mathbf{x})\boldsymbol{\beta}\nabla C(\mathbf{x})\mathbf{v} \]

\(\boldsymbol{\beta}\)是一个对角矩阵，用来衡量各个约束对于能量耗散的贡献程度。这种形式的耗散是能产生的力的作用:

\[ \mathbf{F}=-\nabla_{\mathbf{v}}D = -\nabla C^T(\mathbf{x})\boldsymbol{\beta}\nabla C(\mathbf{x})\mathbf{v} \]

如果这个时候，我们定义一个新的\(\boldsymbol{\mu}:=-\tilde{\boldsymbol{\beta}}\nabla C(\mathbf{x})\mathbf{v}\)，其中\(\tilde{\boldsymbol{\beta}}=\boldsymbol{\beta}\Delta t^2\)，我们就会发现整个过程和上面的推导没有本质的区别，只需要如下的变化：

\[ \mathbf{M}(\mathbf{x}-\tilde{\mathbf{x}})-\nabla C^T(\mathbf{x})(\boldsymbol{\lambda}+\boldsymbol{\mu}) = 0 \\ C(\mathbf{x})+\tilde{\boldsymbol{\alpha}}\tilde{\boldsymbol{\beta}}\nabla C(\mathbf{x})\mathbf{v}+\tilde{\boldsymbol{\alpha}}(\boldsymbol{\lambda}+\boldsymbol{\mu}) = 0 \]

如果我们将\(\boldsymbol{\lambda}+\boldsymbol{\mu} \to \lambda; \mathbf{v}=\frac{\mathbf{x}-\mathbf{x}_{n}}{\Delta t}\)这样看待，去线性化上面的方程同时使用相同的近似条件，我们会得到:

\[ \left[\begin{array}{cc}\mathbf{M}  & -\nabla C^T(\mathbf{x}^i) \\ \nabla C(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}}\tilde{\boldsymbol{\beta}}\nabla C(\mathbf{x})\frac{1}{\Delta t}  & \tilde{\boldsymbol{\alpha}}\end{array}\right]\left[\begin{array}{c}\Delta\mathbf{x}\\ \Delta\boldsymbol{\lambda}\end{array}\right]=-\left[\begin{array}{c}0\\ C(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}}\boldsymbol{\lambda}^i+\tilde{\boldsymbol{\alpha}}\tilde{\boldsymbol{\beta}}\nabla C(\mathbf{x}^i)\frac{\mathbf{x}^i-\mathbf{x}_n}{\Delta t} \end{array}\right] \]

当然这个时候，如果继续使用作者上面奇怪的处理方式，可以得到\(\Delta\boldsymbol{\lambda}\)每个分量上的更细法则:

\[ \Delta\boldsymbol{\lambda}_j=\frac{-C_j(\mathbf{x}^i)-\tilde{\boldsymbol{\alpha}}_j\boldsymbol{\lambda}_j^i-\boldsymbol{\gamma}_j\nabla C(\mathbf{x}^i)(\mathbf{x}^i-\mathbf{x}_n)}{(1+\boldsymbol{\gamma}_j)\nabla C_j(\mathbf{x}^i)M^{-1}\nabla C_j^T(\mathbf{x}^i)+\tilde{\boldsymbol{\alpha}}_j} \]

这边\(\boldsymbol{\gamma}_j=\frac{\tilde{\boldsymbol{\alpha}_j}\tilde{\boldsymbol{\beta}_j}}{\Delta t}\)

Constraints

这个章节，我们将介绍几种常见的约束条件，以及其常见的更新条件，即主要给出约束条件关于坐标的梯度表达式。

Length Constraint(Stretch Constraint)

长度的约束，用来保证相邻两点之间的长度和初始长度接近，因此可以描述成如下的方式:

\[ C(\mathbf{x}_i,\mathbf{x}_j):=\|\mathbf{x}_i-\mathbf{x}_j\|-l_{ij} = 0 \]

\[\nabla_{\mathbf{x}_i}C(\mathbf{x}_i,\mathbf{x}_j)=\frac{\mathbf{x}_i-\mathbf{x}_j}{\|\mathbf{x}_i-\mathbf{x}_j\|}\]

Bend Constraint

Bend Constaint 用来两个相邻三角形之间的夹角接近初始的夹角。

假设两个三角形公共的边为\(\mathbf{x}_1\to\mathbf{x}_2\)，其中第一个三角形另外一个顶点为\(\mathbf{x}_3\)，第二个三角形的另外一个顶点为\(\mathbf{x}_4\),那么可以定义我们的约束条件为下面的形式:

\[ C(\mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_3,\mathbf{x}_4):=\arccos\left(\frac{\mathbf{p}_2\times\mathbf{p}_3}{\|\mathbf{p}_2\times\mathbf{p}_3\|}\cdot\frac{\mathbf{p}_2\times\mathbf{p}_4}{\|\mathbf{p}_2\times\mathbf{p}_4\|}\right)-\theta:=\arccos I - \theta \]

这边\(\mathbf{p}_2:=\mathbf{x}_2-\mathbf{x}_1,\mathbf{p}_3:=\mathbf{x}_3-\mathbf{x}_1,\mathbf{p}_4:=\mathbf{x}_4-\mathbf{x}_1\).

对于这个复杂表达式子，我们要想获得其对应的梯度，核心则需要计算下面的子表达式的梯度，其他的则使用链式法则就可以，(这边为了方便省去了粗体)。

\[ \nabla_x \frac{(x\times y)\cdot z}{\|x\times y\|}=\nabla_x \frac{(y\times z)\cdot x}{\|x\times y\|}=\left(x\cdot(y\times z)\right)\left(\nabla_x\frac{1}{\|x\times y\|}\right)+\frac{y\times z}{\|x\times y\|} \]

\(\nabla_x\|x\times y\|=\frac{\nabla_x\left((x\times y)\cdot(x\times y)\right)}{2\|x\times y\|}=\frac{y\times(x\times y)}{\|x\times y\|}:=y\times n\) 这边我们定义\(n:=\frac{x\times y}{\|x\times y\|}\)，那么

\[ \nabla_x \frac{(x\times y)\cdot z}{\|x\times y\|}=\frac{(n\cdot z)(n\times y)+y\times z}{\|x\times y\|} \]

那么我们定义:

\[ \mathbf{n}_1:=\frac{\mathbf{p}_2\times\mathbf{p}_3}{\|\mathbf{p}_2\times\mathbf{p}_3\|};\mathbf{n}_2:=\frac{\mathbf{p}_2\times\mathbf{p}_4}{\|\mathbf{p}_2\times\mathbf{p}_4\|} \]

1. \[\nabla C = -\frac{1}{\sqrt{1-I^2}}\nabla I\]
2. \[\nabla_{\mathbf{x}_3}I=-\frac{I\mathbf{n}_1\times\mathbf{p}_2+\mathbf{p}_2\times\mathbf{n}_2}{\|\mathbf{p}_2\times\mathbf{p}_3\|}\]
3. \[\nabla_{\mathbf{x}_4}I=-\frac{I\mathbf{n}_2\times\mathbf{p}_2+\mathbf{p}_2\times\mathbf{n}_1}{\|\mathbf{p}_2\times\mathbf{p}_4\|}\]
4. \[\nabla_{\mathbf{x}_2}I=\frac{I\mathbf{n}_1\times\mathbf{p}_3+\mathbf{p}_3\times\mathbf{n}_2}{\|\mathbf{p}_2\times\mathbf{p}_3\|}+\frac{I\mathbf{n}_2\times\mathbf{p}_4+\mathbf{p}_4\times\mathbf{n}_1}{\|\mathbf{p}_2\times\mathbf{p}_4\|}\]
5. \[\nabla_{\mathbf{x}_1}I=-\nabla_{\mathbf{x}_2}I-\nabla_{\mathbf{x}_3}I-\nabla_{\mathbf{x}_4}I\]