Diffusion map method

本篇介绍一种半监督的算法，以及其在理论物理里面的应用

引言

这篇的Blog的源于，最近读到了一篇PRL的paper《Unsupervised machine learning of quantum phase transitions using diffusion maps》 (https://arxiv.org/pdf/2003.07399.pdf)。这篇文章使用了DMM（diffusion map method）来分析量子相变的一些特性，还是蛮有意思的，我会在这边Blog介绍完DMM方法之后，大概说一下其中的一些想法。

在打开这篇paper之前，在我陈旧的机器学习知识框架里，确实没有DMM这个东西，然后我就去好奇去Google了一下，大概发现了两篇有用的paper。

第一篇是2005年PNAS（https://www.pnas.org/doi/epdf/10.1073/pnas.0500334102)，由Yale几位科学家提出来的，将DMM用来做调和分析的工具。
第二篇(https://inside.mines.edu/~whereman/papers/delaPorte-Herbst-Hereman-vanderWalt-PRASA-2008.pdf)是一篇不错的tutorial性质的文章。

读完这些，DMM这个方法让我惊艳的地方，一句话大概是：

NOTE 从局部性质衍生全局性质，进而进行分析的一种算法

正如第一篇PNAS中所说：

The process of iterating or diffusing the Markov matrix is seen as a generalization of some aspects of the Newtonian paradigm, in which local infinitesimal transitions of a systemlead to global macroscopic descriptions by integration.

DMM(Difussion map method)

算法DMM大概用两种用途：

数据降维
聚类

当然一个算法如果能很好地对数据进行降维，额外做数据的聚类也是一个简单的任务，比如结合K-Means等等这种常规算法。下面我们就主要介绍降维方面的一些想法

现有的算法

PCA

提到数据降维，我想作为炼丹师，一下能够想到很多出名的算法，其中不得不说，非PCA(principal component analysis)莫属。当然PCA是一个线性算法。这可以从几方面来理解。 - 从代数的角度，PCA 算法用到的操作都是一个线性空间的线性操作 - 从几何的角度，PCA 只是通过旋转坐标轴的，找到那些数据高区分度的坐标轴进行保留。

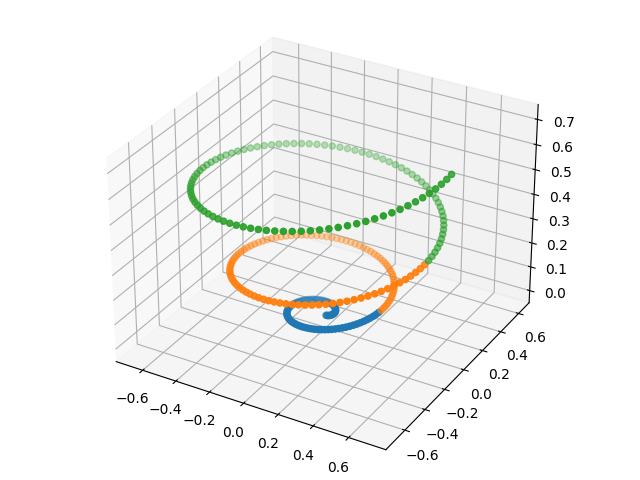
这其中最关键的，所谓的在线性空间进行线性操作，无论怎么搞，坐标轴永远是“直”的。但是我们知道，比如我空间里一条曲线，在“直”的坐标系下面仍然需要三个坐标去描述，但是实际上，一条曲线的有效的维度永远是一维的（当然这边描述不够严谨，比如也是有一些奇怪的曲线维度是分数维的，这边只是对于那种普通的曲线，供大家理解）。例如，下面这条曲线上，我用三种颜色表示了三个聚类，在这种数据下，我们是没有办法使用PCA去做数据降维或者聚类分析。

MDS(Mutidimensional Scaling)

算法MDS的idea，我觉得是非常棒的，比PCA更加自然，也是如果一个没有学过机器学习的人，让他来做数据降维，最容易想到的一个做法。这边我们简单描述这个想法：

假设我们有个\(N\)个数据点\(x_i\)，我们需要找一个map，将每个\(x_i\)映射到\(y_i\)，还尽可能保留数据之间的"关系"。比如找到一种数据描述\(d_X,d_Y\)来建模这种"关系"。那么对于任意\(d_X(x_i,x_j)\)，我们希望\(d_X(x_i,x_j)\)小(大)的，映射之后对应的关系\(d_Y(y_i,y_j)\)也小(大)。

当然MDS采用了欧式距离来建模这种“关系”，这也是这个方法的局限，毕竟欧式距离做为线性结构的度量是不错的，但是如果数据之间的关系是非线性的，那么欧式距离只是在邻域内看作是一个相对有效的表达。

DMM

那么在我们不知道数据的几何结构的时候（如果知道，只需要拟合即可，问题就会简单了），我们如果才能如何有效地表达出\(d_X, d_Y\)呢。DMM提出了一个核心想法：

通过扩散过程，衔接局部性质和全局性质

这种想法在物理研究其实很常见：

牛顿力学或是量子力学都是通过建立微分方程(局部)，然后积分求解，得到一些宏观的可观测量(全局)
蒙特卡洛模拟，也是使用局部的概率进行模拟，通过Hamiltonian带来的相互作用，将整个影响传播至全局，最后得一个平衡态。
等等

在DMM算法中通过一个核函数\(k(x_i,x_j)\)来模拟原始数据之间的局部关系，比如常用的高斯核\(k(x_i,x_j) = e^{-\frac{\|x_i-x_j\|^2}{2\epsilon}}\)。拥有了核函数对应的矩阵\(K_{ij}:=k(x_i,x_j)\)，我们可以对每一行进行归一化，得到一个符合转移矩阵的要求矩阵\(P:=D^{-1}K\)，这边\(D\)是一个对角矩阵，每个元素是对应行的\(K\)矩阵的元素之和。那么这个扩散过程，我们就可以通过\(P, P^2, P^3, \cdots, P^t, \cdots\)来模拟。假设我们模拟了\(t\)步，概率流在这个图中流淌了一段时间，局部的性质通过这种流淌，慢慢全局化。那么这时候需要一个问题，在这种建模的情况，我们如何去描述第\(i\)和\(j\)数据之间的关系呢？回答好这个问题，那么DMM的算法就完毕了，剩余的只是一些不那么关键的数学推导了。在当前的建模情况，\(P\)矩阵的第\(i\)行表示的第\(i\)组数据和其他数据之间的转移概率。那么描述\(i\)和\(j\)的相似度，其实就变得很简单了，就是描述两个概率分布之间的相似度。最常见的两种就是：

L2 \(\sum_k |P^t_{ik}-P^t_{jk}|^2\)
CrossEntropy \(-\sum_k P^t_{ik}\log P^t_{jk}\)

当然在DMM算法中他选择了第一种描述关系，这是为了他做数据降维方便而做的选择。正如我们之前说的L2是一个描述线性结构的度量方式，选择了\(L2\)就是采用数据经过扩散过程之后，局部的关系变成了全局的关系，并且全局的关系进入了一个相对平坦的子流形上去了。

这边我自己也很好奇，如果我选用第二种相似度描述方式，该如何去做数据降温呢？

到了这一步，我们拥有了一个数据的有效表示\(P^t_{i*}\)，同时还假设了线性，那么这个时候使用什么方式去做数据降维那么就是显而易见了，我们只需要对\(P^t\)做一次PCA，就可以做到了。当然了在原始的paper，研究人员使用了一些数学手段简化了这个PCA过程，有兴趣的可以看看附录吧。

到了这边，有了数据表示和数据相似度的数学建模，那么除了数据降维，去做一个聚类任务也是比较简单的事情了。比如对上面的那组测试数据，我们使用DMM降三维数据降到二维，得到下面的结果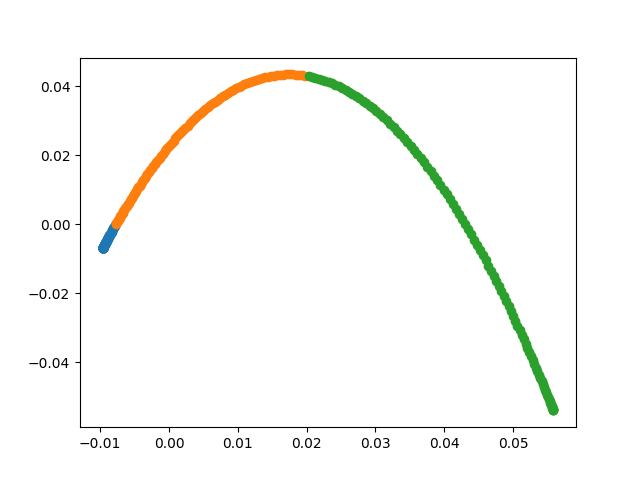我们很容易得出下面两点结论：

数据的order得到了保证，蓝-橘-绿
数据变得更加的紧致

如果降维到一维的结果，就是把上面这个图向\(x\)轴投影，我们会发现上面的两点结论仍然是成立的。这个Demo的例子可以用下面这段生成

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

def gaussian_kernel(point1, point2, alpha: float = 0.01):
    return np.exp(-np.linalg.norm(point1 - point2)**2 / alpha)


class DiffusionMap:
    """
    a simple realization of diffusion map method
    """
    def __init__(self):
        pass

    @staticmethod
    def diff_map(data: np.ndarray, kernel_func, keep_dim: int = 2):
        """
        Params:
        -------------------
        data: N x M numpy array, N data points with original dimension M
        kernel_func: a function, give the measure between two data points
        keep_dime: int, the number of dimension left
        """
        data_num = data.shape[0]
        kernel_mat = np.zeros((data_num, data_num))
        for i in range(data_num):
            for j in range(data_num):
                kernel_mat[i, j] = kernel_func(data[i, :], data[j, :])
        normalize_mat = np.diag(np.sum(kernel_mat, axis=1))
        normalize_mat_sqrt = np.sqrt(normalize_mat)
        normalize_mat_sqrt_inv = np.linalg.inv(normalize_mat_sqrt)
        transition_mat_sim = normalize_mat_sqrt_inv.dot(kernel_mat).dot(normalize_mat_sqrt_inv)
        print("symmetry error:", np.sum(np.abs(transition_mat_sim - transition_mat_sim.T)))
        # transition_mat = kernel_mat / np.sum(kernel_mat, axis=1, keepdims=True)
        eig_vals, eig_vecs_sim = np.linalg.eig(transition_mat_sim)
        # print("eig_vals:", eig_vals)
        eig_vals_sort = np.sort(eig_vals)[::-1]
        eig_vals_sort_index = np.argsort(eig_vals)[::-1]
        eig_vecs_tran = normalize_mat_sqrt_inv.dot(eig_vecs_sim)
        if keep_dim > data_num - 1:
            keep_dim = data_num - 1
        diffusion_map = np.zeros((data_num, keep_dim))
        for i in range(keep_dim):
            val = eig_vals_sort[i+1]
            eig_vec = eig_vecs_tran[:, eig_vals_sort_index[i+1]]
            print("norm:", np.linalg.norm(eig_vec))
            diffusion_map[:, i] = val * eig_vec
        return diffusion_map

if __name__ == "__main__":
    n = 300
    r = np.linspace(0, 1, n)
    theta = np.linspace(0, 6 * np.pi, n)
    phi = np.linspace(0, np.pi / 4, n)
    x = r * np.cos(theta) * np.cos(phi)
    y = r * np.sin(theta) * np.cos(phi)
    z = r * np.sin(phi)
    fig1 = plt.figure()
    ax1 = Axes3D(fig1)
    ax1.scatter(x[:100], y[:100], z[:100])
    ax1.scatter(x[100:200], y[100:200], z[100:200])
    ax1.scatter(x[200:], y[200:], z[200:])
    data = np.concatenate([x.reshape(-1,1), y.reshape(-1,1), z.reshape(-1,1)], axis=1)
    reduce_data = DiffusionMap.diff_map(data, gaussian_kernel)
    fig2 = plt.figure()
    plt.scatter(reduce_data[:100,0], reduce_data[:100,1])
    plt.scatter(reduce_data[100:200,0], reduce_data[100:200,1])
    plt.scatter(reduce_data[200:,0], reduce_data[200:,1])
    plt.show()

使用DMM研究量子相变

这边主要是展示一下之前那篇PRL的其中之一的一个工作。在这边文章中，作者使用DMM来做聚类任务，认为类别的数目可以作为一个宏观的量来描述各种物理相。

首先，咱们先把物理抛在脑后，先思考一个问题\(\epsilon\)和聚类的数目的关系应该是什么样子的。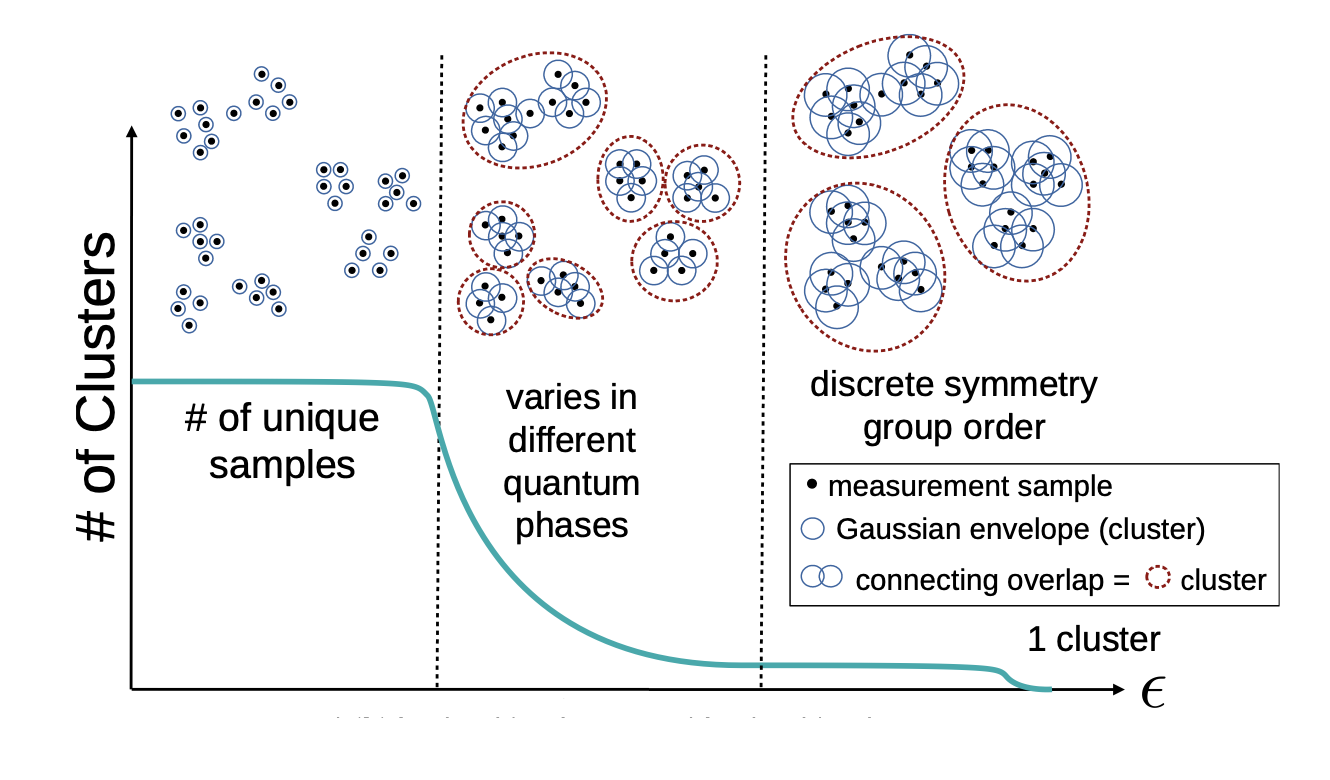

特征半径和聚类数目的关系

如上图中蓝线所示，我们可以想象，当\(\epsilon\)很小的时候，核函数衰减得非常快，那么每个数据点，就很容易被隔离开，自己单独形成一个聚类。随着\(\epsilon\)的慢慢增大，一些相近的数据点之间的连接逐渐形成，那么聚类开始成团簇状。直到\(\epsilon\)变得很大，核函数在整个尺度都不怎么衰减，所有数据点构成一个团簇。显然，中间的这种状态是比较有意思的情况，两端的情况则相对trivial。

下面作者用了一个理论物理常用的模型， \(Z_3\)的横场Ising模型，哈密顿量可以写成下面这种形式: \[ H = -f \sum_{j=1}^N \tau_j e^{i\theta} - (1 - f)\sum_{j=1}^N \sigma_j \sigma_{j+1}^{\dagger}e^{i\theta} + h.c. \] 众所周知，这个模型： - 在没有手性的情况(\(\theta=0\))，有两个相，铁磁相和顺磁相。 - 在有手性的情况(\(\theta > 0\)), 在铁磁和顺磁之间，还有一个额外的相IC(incommensurate phase, 我也不知道中文是啥)。这个中间相不同铁磁和顺磁那么好区分。因为它的自发磁化强度也是0，因此\(\sum_{j=1}^N \langle \sigma_j \rangle\) 作为一个宏观可观测量，不足以区分这两种相。

这边作者通过测量哈密顿量对应的基态对应的磁化强度，得到了一些数据点\(\vec{M}_i\)，然后通过对这些数据点，使用DMM做聚类分析，画出了不同的参数\(f,\theta\)下面，对应的聚类数目密度图，惊喜地发现（如图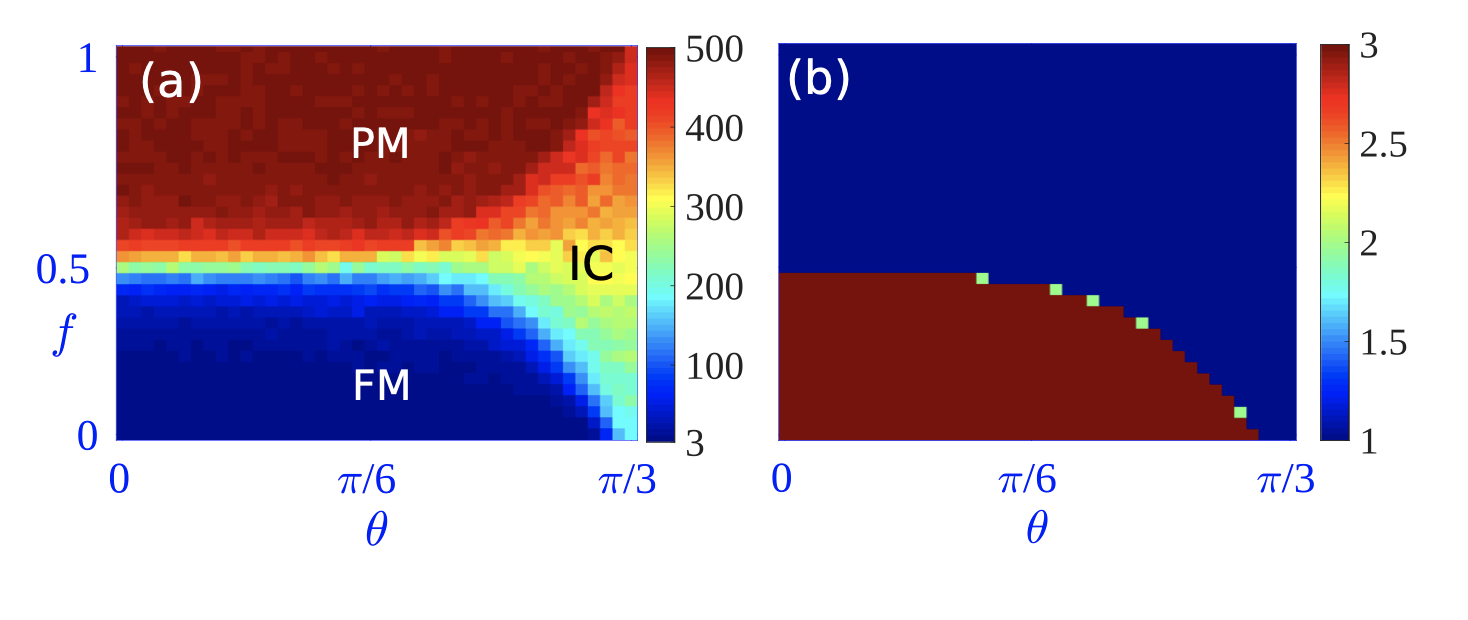）： - 选择不同的\(\epsilon\) 可以得到不同的相图 - 选择合适的\(\epsilon\)，可以很好根据聚类的数目，区分出来三种相，和物理的结果吻合。

DMM数学简化

对于给定的一个核矩阵\(K\)，我们可以得到转移矩阵\(P=D^{-1}K\)，正如之前说的。显然，\(P\)在大部分的情况下，都不是一个实对称的矩阵，我们可以通过简单的转化，分析\(Q = D^{-\frac{1}{2}}KD^{-\frac{1}{2}}\)来探索\(P\)的一些性质。很显然，

\(P\)和\(Q\)是一对相似矩阵
\(Q\)是实对称的

那么我们可以轻松地在实数域内，对\(Q\)做对角化，得到其对应的特征值\(1=\lambda_0\ge \lambda_i \ge \cdots \ge \lambda_{N-1} \ge 0\) 和对应的特征向量\(v_0, v_1, \cdots, v_{N-1}\)。那么我们很容易发现\(P\)矩阵的右特征向量为\(u_0:=D^{-\frac{1}{2}}v_0, u_1:=D^{-\frac{1}{2}}v_1, \cdots\) 和左特征向量 \(w_0 := D^{\frac{1}{2}}v_0, w_1 = D^{\frac{1}{2}}v_1, \cdots\)。那么\(P\)的谱分解可以写成： \[ P = \sum_{j=0}^{N-1}\lambda_j u_j w_j^T \] 同时\(t\)-step 的转移矩阵可以写成: \[ P^t = \sum_{j=0}^{N-1}\lambda_j^t u_j w_j^T \] 那么在\(\{w_j\}_{j=1}^{N-1}\)构成的坐标系下面，第\(i\)组数据的表达就是\((\lambda_0^t u_0(i), \lambda_1^t u_1(i), \cdots, \lambda_{N-1}^t u_{N-1}(i))\)。使用者可以根据需求对\(0\)到\(N-1\)之间的dimension选择适合的维度进行，然后做数据降维。

AnsChen's Home

Diffusion Map Method