Bolza问题
引言
最近在学习The financial mathematics of market liquidity 和游戏中物理模拟的一些知识，发现这两个地方都涉及到了Bolza问题，决定单独把这块提取出来说一说。我们这边主要把Bolza问题集中在最小化这个小问题上面: \[ J = \int_{0}^T f_t(x(t)) + g_t(\dot{x}(t))dt \] 并且满足边界条件\(x(0) = a, x(T) = b\)。
当然更加一般的Bolza问题可以参考这个链接 https://encyclopediaofmath.org/wiki/Bolza_problem 这边我们考虑是其简化版本，在一般的兼容建模和物理模拟中足够使用了。
NOTE 笔者背景偏理论物理向，所以整个Blog在数学上可能不是那么严谨，但求能够讲清楚其背后的一些原理性的东西
最速降线
看到上面那个带优化的方程，对于学过一些物理的朋友来说，第一反应就是联想到Lagrangian。那么这边我们就从经典的最速降线说起。最速降线要解决的一个问题就是，在纯重力场下面，找到一条轨道，使得从点A到点B(点A高度高于点B)，用的时间最短。如图所示 显然，我们要优化的东西是 \(T=\int_0^T dt\)，通过简单的运动学和能量守恒，我们就可以得到， \[ dt = \frac{\sqrt{dx^2 + dy^2}}{v} = \frac{\sqrt{1+y'^2(x)}}{\sqrt{2gy}}dx \] 因此我们最终的优化问题是： \[ J[y(x)] = \int_{x_A}^{x_B}\frac{\sqrt{1+y'^2(x)}}{\sqrt{2gy}}dx \] 从这边我们可以看出来，最速降线就是一种Bloza问题～
Legendre变换
提到Legendre变换，我想对于物理系毕业的学生，一下就会想到理论力学和热力学学到的两个场景
理论力学
众所周知，理论力学有两套描述方式，一套走的拉格朗日力学，一套走的哈密顿力学。从广义坐标和虚功原理出发，我们可以很容易找到在保守场中动力学描述： \[ L = T(q,\dot{q})- V(q) \]， 这边\(q, T, V\)分别代表系统的广义坐标，动能，保守势能。动力学对应的微分方程是 \[ \frac{d}{dt}\frac{\partial L}{\partial \dot{q}_k} = \frac{\partial L}{\partial q_k} \]
哈密顿力学则可以通过Legendre变换，从拉格朗日力学中转变而来， \[ \dot{p}_k = -\nabla_{q_k}H(p,q), \dot{q}_k = \nabla_{p_k}H(p,q) \] 这边动量\(p:=\frac{\partial L}{\partial \dot{q}_k}\)，而哈密顿量\(H\)则是拉格朗日量通过Legendre变换得来 \(H = p^T \dot{q} - L(q, \dot{q})\)。
热力学
在热力学中，我们知道有几个基本的物理量，焓\(H\), 哪能\(U\), 亥姆霍兹自由能\(F\)，吉布斯自由能\(G\)，满足下面的关系 \[ H = U + PV, G = H - TS, A = U - TS \] 这边\(T,S\) 代表系统的温度和熵，\(P,V\)代表系统的压强和体积。 笔者，当初在学习热力学的时候，对于\((T,S), (P,V)\)这两组共轭变量，也是只是认为量纲互补，也是最近才理解了这边共轭的来源，惭愧...
数学
数学上对于Legendre变换的定义如下：
定义 如果函数\(f(x): R^d \to R\) 在我们所关心的区域内是可导的，函数\(f(x)\)对应的Legendre变换定义为 \[ f^*(p) = p^T x - f(x) |_{\frac{d(px-f(x))}{dx} = 0} \]
从图上我们可以看到Legendre变换的几何意义: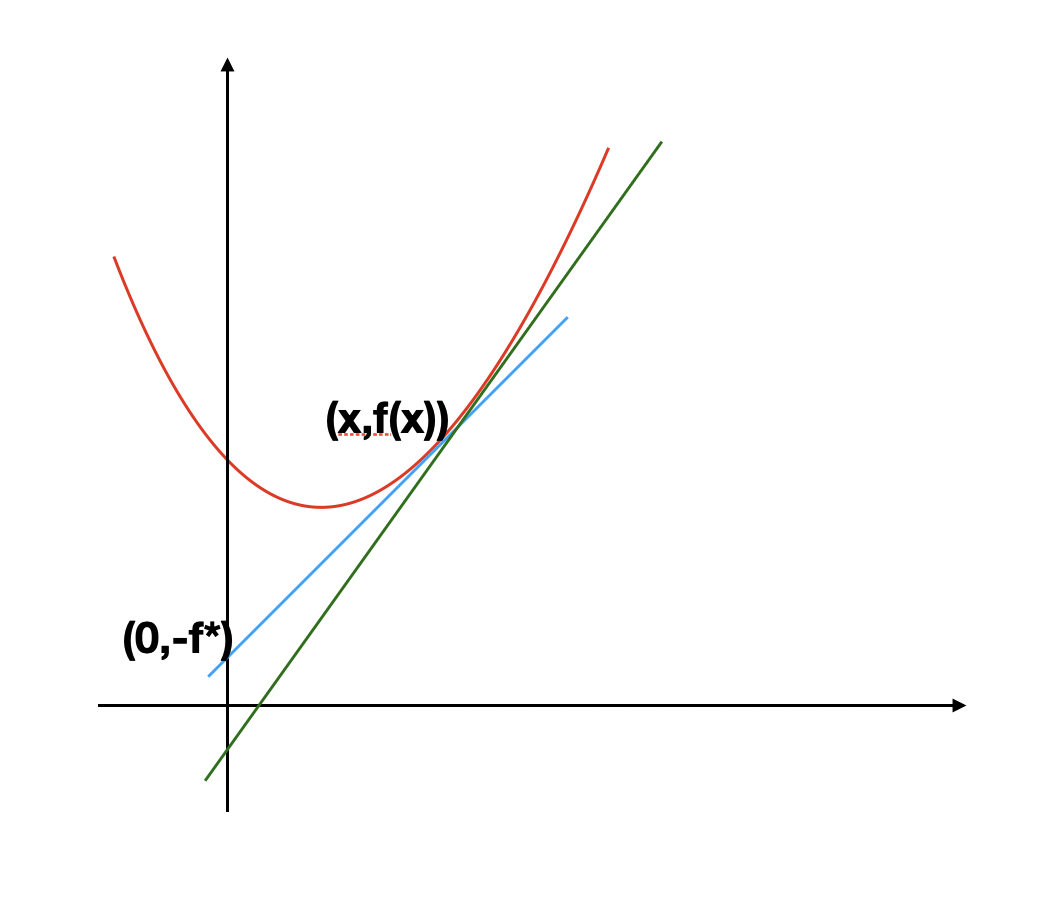 
从这定义，我们可以看出来，加入\(f(x)\)一个满足超线性\(\lim_{|x|\to\infty}\frac{|f(x)|}{|x|} = \infty\)的凸函数，那么这个定义等价于 \[
f^*(p) = \sup_{x} p^T x - f(x)
\] 对着演示的这幅图，我们可以想象，比如\(x\)越来越大的时候，\(f(x)\)增加越来越快，对应的切线变陡峭的速率也越来越快，\(f^*\) 增加得也越来越快。因此，我们可以claim，数学证明也是很简单的，在这边就不赘述了。
性质 \(f^*\)也是一个凸函数
对比上面两种物理，尤其是理论力学中的结构，我们可以任何一个拉格朗日量，对应的哈密顿量也会继承其的凹凸性，这点是非常重要有意思的，有兴趣的读者可以脑子里想象一下简单的弹簧系统。